题目内容
(a-c):(a+b):(c-b)=2:7:1,且a+b+c=20,则a=________,b=________,c=________.
10 4 6
分析:由(a-c):(a+b):(c-b)=2:7:1,可设a-c=2k,a+b=7k,c-b=k,则可求得a,b,c用k表示的值,又由a+b+c=20,求得k的值,则可求得a,b,c的值.
解答:∵(a-c):(a+b):(c-b)=2:7:1,
∴设a-c=2k,a+b=7k,c-b=k,
∴a=5k,b=2k,c=3k,
∵a+b+c=20,
∴5k+2k+3k=20,
解得:k=2,
∴a=10,b=4,c=6.
故答案为:10,4,6.
点评:此题考查了比例的性质与方程组的解法.此题难度适中,解题的关键是注意掌握由(a-c):(a+b):(c-b)=2:7:1,可设a-c=2k,a+b=7k,c-b=k的解题方法.
分析:由(a-c):(a+b):(c-b)=2:7:1,可设a-c=2k,a+b=7k,c-b=k,则可求得a,b,c用k表示的值,又由a+b+c=20,求得k的值,则可求得a,b,c的值.
解答:∵(a-c):(a+b):(c-b)=2:7:1,
∴设a-c=2k,a+b=7k,c-b=k,
∴a=5k,b=2k,c=3k,
∵a+b+c=20,
∴5k+2k+3k=20,
解得:k=2,
∴a=10,b=4,c=6.
故答案为:10,4,6.
点评:此题考查了比例的性质与方程组的解法.此题难度适中,解题的关键是注意掌握由(a-c):(a+b):(c-b)=2:7:1,可设a-c=2k,a+b=7k,c-b=k的解题方法.

练习册系列答案
相关题目
 如图,已知AB是⊙O的直径,AC与⊙O相切于点A,CO交⊙O于点D,BD的延长线交AC于点E,求证:AB•CD=AC•AE.
如图,已知AB是⊙O的直径,AC与⊙O相切于点A,CO交⊙O于点D,BD的延长线交AC于点E,求证:AB•CD=AC•AE.
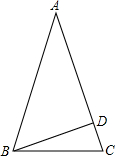 已知:如图,在△ABC中,AB=AC,∠C=2∠A,BD⊥AC于D.
已知:如图,在△ABC中,AB=AC,∠C=2∠A,BD⊥AC于D. 在△ABC中,AD交BC于点D,E、F和G分别是边AB、AC和AD上的点,且BE=GF=AF,FG∥BE,连接BG,EF.
在△ABC中,AD交BC于点D,E、F和G分别是边AB、AC和AD上的点,且BE=GF=AF,FG∥BE,连接BG,EF. ,试说明△ABG∽△AGF.
,试说明△ABG∽△AGF. 如图,在Rt△ABC中,已知∠ACB=90°,且CH⊥AB,HE⊥BC,HF⊥AC.
如图,在Rt△ABC中,已知∠ACB=90°,且CH⊥AB,HE⊥BC,HF⊥AC.