题目内容
 如图,已知AB是⊙O的直径,AC与⊙O相切于点A,CO交⊙O于点D,BD的延长线交AC于点E,求证:AB•CD=AC•AE.
如图,已知AB是⊙O的直径,AC与⊙O相切于点A,CO交⊙O于点D,BD的延长线交AC于点E,求证:AB•CD=AC•AE.
证明:连接AD,
∵AB是⊙O的直径,
∴AD⊥BE.
∵AC是⊙O的切线,
∴∠EAD=∠B.
∵BO=DO,
∴∠B=∠ODB=∠EDC,
∴∠EAD=∠EDC.
又∠C=∠C,∴△ACD∽△DCE,∴ =
= ;
;
在Rt△AEB中,AD⊥BE,∠EAD=∠B,
∴△AED∽△BEA,
∴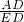 =
= ,
,
∴ =
= .
.
∴AB•CD=AC•AE.
分析:连接AD.要证AB•CD=AC•AE,即证 =
= .由△ACD∽△DCE,可得
.由△ACD∽△DCE,可得 =
= ;由△AED∽△BEA,可得
;由△AED∽△BEA,可得 =
= .
.
 =
= .即可得出AB•CD=AC•AE.
.即可得出AB•CD=AC•AE.
点评:根据乘积的形式通常可以转化为比例的形式,本题可以通过两组相似三角形的性质得出的比例式综合应用即可证明.
∵AB是⊙O的直径,
∴AD⊥BE.
∵AC是⊙O的切线,
∴∠EAD=∠B.
∵BO=DO,
∴∠B=∠ODB=∠EDC,
∴∠EAD=∠EDC.
又∠C=∠C,∴△ACD∽△DCE,∴
 =
= ;
;在Rt△AEB中,AD⊥BE,∠EAD=∠B,
∴△AED∽△BEA,
∴
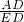 =
= ,
,∴
 =
= .
.∴AB•CD=AC•AE.
分析:连接AD.要证AB•CD=AC•AE,即证
 =
= .由△ACD∽△DCE,可得
.由△ACD∽△DCE,可得 =
= ;由△AED∽△BEA,可得
;由△AED∽△BEA,可得 =
= .
. =
= .即可得出AB•CD=AC•AE.
.即可得出AB•CD=AC•AE.点评:根据乘积的形式通常可以转化为比例的形式,本题可以通过两组相似三角形的性质得出的比例式综合应用即可证明.

练习册系列答案
相关题目
 如图,已知AB是⊙O的直径,AC是弦,D为AB延长线上一点,DC=AC,∠ACD=120°,BD=10.
如图,已知AB是⊙O的直径,AC是弦,D为AB延长线上一点,DC=AC,∠ACD=120°,BD=10. 如图,已知AB是⊙O的直径,C是⊙O上一点,∠BAC的平分线交⊙O于点D,交⊙O的切线BE于点E,过点D作DF⊥AC,交AC的延长线于点F.
如图,已知AB是⊙O的直径,C是⊙O上一点,∠BAC的平分线交⊙O于点D,交⊙O的切线BE于点E,过点D作DF⊥AC,交AC的延长线于点F. (2013•泰安)如图,已知AB是⊙O的直径,AD切⊙O于点A,点C是
(2013•泰安)如图,已知AB是⊙O的直径,AD切⊙O于点A,点C是
 如图,已知AB是⊙O的直径,P为⊙O外一点,且OP∥BC,∠P=∠BAC.
如图,已知AB是⊙O的直径,P为⊙O外一点,且OP∥BC,∠P=∠BAC. 如图,已知AB是圆O的直径,∠DAB的平分线AC交圆O与点C,作CD⊥AD,垂足为点D,直线CD与AB的延长线交于点E.
如图,已知AB是圆O的直径,∠DAB的平分线AC交圆O与点C,作CD⊥AD,垂足为点D,直线CD与AB的延长线交于点E.