题目内容
 在△ABC中,AD交BC于点D,E、F和G分别是边AB、AC和AD上的点,且BE=GF=AF,FG∥BE,连接BG,EF.
在△ABC中,AD交BC于点D,E、F和G分别是边AB、AC和AD上的点,且BE=GF=AF,FG∥BE,连接BG,EF.
(1)试说明AD平分∠BAC.
(2)若AB=4,AG=3,BE= ,试说明△ABG∽△AGF.
,试说明△ABG∽△AGF.
证明: (1)∵GF=AF,
(1)∵GF=AF,
∴∠FAG=∠FGA,
∵FG∥BE,
∴∠BAD=∠AGF,
∴∠FAG=∠BAD,
即AD平分∠BAC;
(2)∵BE=GF=AF,
∴AF= ,
,
∵AB=4,AG=3,BE= ,
,
∴ =
= ,
,
又∵∠FAG=∠BAD,
∴△ABG∽△AGF.
分析:(1)根据等边对等角以及平行线的性质得出∠FAG=∠FGA以及∠BAD=∠AGF即可得出答案;
(2)利用已知得出 =
= ,以及利用(1)中结论,得出△ABG∽△AGF.
,以及利用(1)中结论,得出△ABG∽△AGF.
点评:此题主要考查了相似三角形的判定与平行线的性质,根据已知得出 =
= 是解题关键.
是解题关键.
 (1)∵GF=AF,
(1)∵GF=AF,∴∠FAG=∠FGA,
∵FG∥BE,
∴∠BAD=∠AGF,
∴∠FAG=∠BAD,
即AD平分∠BAC;
(2)∵BE=GF=AF,
∴AF=
 ,
,∵AB=4,AG=3,BE=
 ,
,∴
 =
= ,
,又∵∠FAG=∠BAD,
∴△ABG∽△AGF.
分析:(1)根据等边对等角以及平行线的性质得出∠FAG=∠FGA以及∠BAD=∠AGF即可得出答案;
(2)利用已知得出
 =
= ,以及利用(1)中结论,得出△ABG∽△AGF.
,以及利用(1)中结论,得出△ABG∽△AGF.点评:此题主要考查了相似三角形的判定与平行线的性质,根据已知得出
 =
= 是解题关键.
是解题关键. 
练习册系列答案
 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案
相关题目
 23、如图,在△ABC中,AD交边BC于点D,∠BAD=15°,∠ADC=4∠BAD,DC=2BD.
23、如图,在△ABC中,AD交边BC于点D,∠BAD=15°,∠ADC=4∠BAD,DC=2BD. 在△ABC中,AD交BC于点D,E、F和G分别是边AB、AC和AD上的点,且BE=GF=AF,FG∥BE,连接BG,EF.
在△ABC中,AD交BC于点D,E、F和G分别是边AB、AC和AD上的点,且BE=GF=AF,FG∥BE,连接BG,EF.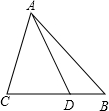 如图,在△ABC中,AD交边BC于点D,∠BAD=15°,∠ADC=4∠BAD,DC=2BD.
如图,在△ABC中,AD交边BC于点D,∠BAD=15°,∠ADC=4∠BAD,DC=2BD. ,试说明△ABG∽△AGF.
,试说明△ABG∽△AGF.