题目内容
20.某水果商从批发市场用8000元购进了大樱桃和小樱桃各200千克,大樱桃的进价比小樱桃的进价每千克多20元.大樱桃售价为每千克40元,小樱桃售价为每千克16元.(1)大樱桃和小樱桃的进价分别是每千克多少元?销售完后,该水果商共赚了多少元钱?
(2)该水果商第二次仍用8000元钱从批发市场购进了大樱桃和小樱桃各200千克,进价不变,但在运输过程中小樱桃损耗了20%.若小樱桃的售价不变,要想让第二次赚的钱不少于第一次所赚钱的90%,大樱桃的售价最少应为多少?
分析 (1)根据用8000元购进了大樱桃和小樱桃各200千克,以及大樱桃的进价比小樱桃的进价每千克多20元,分别得出等式求出答案;
(2)根据要想让第二次赚的钱不少于第一次所赚钱的90%,得出不等式求出答案.
解答 解:(1)设小樱桃的进价为每千克x元,大樱桃的进价为每千克y元,根据题意可得:
$\left\{\begin{array}{l}{200x+200y=8000}\\{y-x=20}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{x=10}\\{y=30}\end{array}\right.$,
小樱桃的进价为每千克10元,大樱桃的进价为每千克30元,
200×[(40-30)+(16-10)]=3200(元),
∴销售完后,该水果商共赚了3200元;
(2)设大樱桃的售价为a元/千克,
(1-20%)×200×16+200a-8000≥3200×90%,
解得:a≥41.6,
答:大樱桃的售价最少应为41.6元/千克.
点评 此题主要考查了二元一次方程组的应用以及一元一次不等式的应用,正确表示出总费用是解题关键.

练习册系列答案
相关题目
11.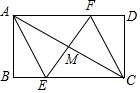 如图,在一张矩形纸片内,先折出矩形的对角线AC,以AC为折痕折叠AD交BC边于点E,再以AC为折痕折叠BC交AD边于点F,则下列结论不一定正确的是( )
如图,在一张矩形纸片内,先折出矩形的对角线AC,以AC为折痕折叠AD交BC边于点E,再以AC为折痕折叠BC交AD边于点F,则下列结论不一定正确的是( )
 如图,在一张矩形纸片内,先折出矩形的对角线AC,以AC为折痕折叠AD交BC边于点E,再以AC为折痕折叠BC交AD边于点F,则下列结论不一定正确的是( )
如图,在一张矩形纸片内,先折出矩形的对角线AC,以AC为折痕折叠AD交BC边于点E,再以AC为折痕折叠BC交AD边于点F,则下列结论不一定正确的是( )| A. | AE=CF | B. | AB=AM | C. | AC⊥EF | D. | EF平分∠AEC |
8.下列图形中,既是轴对称图形又是中心对称图形的是( )
| A. |  | B. |  | C. |  | D. |  |
15.下列4个图形中,是中心对称图形但不是轴对称的图形是( )
| A. |  | B. |  | C. |  | D. |  |
10.下列实数中,为有理数的是( )
| A. | $\sqrt{3}$ | B. | π | C. | $\root{3}{2}$ | D. | 1 |
 如图,方格纸中每个小正方形的边长都是1个单位长度,△ABC在平面直角坐标系中的位置如图所示.
如图,方格纸中每个小正方形的边长都是1个单位长度,△ABC在平面直角坐标系中的位置如图所示.
 一块竹条编织物,先将其按如图所示绕直线MN翻转180°,再将它按逆时针方向旋转90°,所得的竹条编织物是( )
一块竹条编织物,先将其按如图所示绕直线MN翻转180°,再将它按逆时针方向旋转90°,所得的竹条编织物是( )



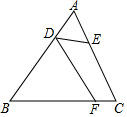 如图,在△ABC中,AB≠AC.D、E分别为边AB、AC上的点.AC=3AD,AB=3AE,点F为BC边上一点,添加一个条件:DF∥AC,或∠BFD=∠A,可以使得△FDB与△ADE相似.(只需写出一个)
如图,在△ABC中,AB≠AC.D、E分别为边AB、AC上的点.AC=3AD,AB=3AE,点F为BC边上一点,添加一个条件:DF∥AC,或∠BFD=∠A,可以使得△FDB与△ADE相似.(只需写出一个)