题目内容
8. 如图,在△ABC中,AD是BC边上的中线.
如图,在△ABC中,AD是BC边上的中线.①画出与△ACD关于D点成中心对称的三角形;
②找出与AC相等的线段;
③若AB=5,AC=3,AD=2,求线段BC的长.
分析 ①利用关于点D成中心对称的性质得出E点位置进而得出答案;
②利用对称的性质得出AC=BE;
③首先得出△ABE是直角三角形,进而利用勾股定理得出答案.
解答 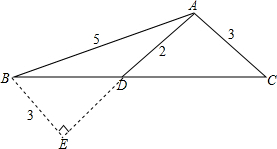 解:①如图所致:
解:①如图所致:
延长AD至E,使DE=AD,连接BE,则△EBD即为所求三角形;
②BE=AC;
③如图所示,由题意可得:AD=DE=2,
则AE=4,
故AB2=BE2+AE2,
则△ABE是直角三角形,
故BD=$\sqrt{B{E}^{2}+D{E}^{2}}$=$\sqrt{13}$,
∴BC=2BD=2$\sqrt{13}$.
点评 此题主要考查了旋转变换以及勾股定理的逆定理,正确利用关于点对称的性质得出对应点位置是解题关键.

练习册系列答案
 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案
相关题目
10.用科学记数法表示28000是( )
| A. | 28×103 | B. | 2.8×103 | C. | 2.8×104 | D. | 2.8×105 |
20.在一幅比例尺为1:500000的地图上,若量得甲、乙两地的距离是25cm,则甲、乙两地实际距离为( )
| A. | 125km | B. | 12.5km | C. | 1.25km | D. | 1250km |
 如图,已知AB=AC,∠B=∠C,则BD=CD,请说明理由.
如图,已知AB=AC,∠B=∠C,则BD=CD,请说明理由. 如图所示,在△ABC中,∠A=90°,∠ABC的平分线与∠ACB的平分线相交于点O,求∠BOC的度数.
如图所示,在△ABC中,∠A=90°,∠ABC的平分线与∠ACB的平分线相交于点O,求∠BOC的度数. 如图,公路AC,BC互相垂直,公路AB的中点M与点C被湖隔开,若测得AM的长为1.2km,则M,C两点间的距离为1.2km.
如图,公路AC,BC互相垂直,公路AB的中点M与点C被湖隔开,若测得AM的长为1.2km,则M,C两点间的距离为1.2km. 如图,一次函数y=kx+b与反比例函数y=$\frac{m}{x}$图象交于A,B两点,与x轴交于点C(-2,0),点A的横坐标为1,S△AOC=2.
如图,一次函数y=kx+b与反比例函数y=$\frac{m}{x}$图象交于A,B两点,与x轴交于点C(-2,0),点A的横坐标为1,S△AOC=2. 如图,在矩形ABCD中,AB=3,BC=4,点E在BC边上运动,连结AE,过点D作DF⊥AE,垂足为F,设AE=x,DF=y,则能反映y与x之间函数关系的大致图象是( )
如图,在矩形ABCD中,AB=3,BC=4,点E在BC边上运动,连结AE,过点D作DF⊥AE,垂足为F,设AE=x,DF=y,则能反映y与x之间函数关系的大致图象是( )



 在美化校园的活动中,某兴趣小组想借助如图所示的直角墙角(两边足够长),用26m长的篱笆围成一个矩形花园ABCD(篱笆只围AB,BC两边),设BC=x m.
在美化校园的活动中,某兴趣小组想借助如图所示的直角墙角(两边足够长),用26m长的篱笆围成一个矩形花园ABCD(篱笆只围AB,BC两边),设BC=x m.