题目内容
11.如图1,△ABC中,点A、B、C三点的坐标分别为A (-1,2$\sqrt{3}$),B (-3,0),C (-1,0);如图2,将△ABC绕点C顺时针旋转∠α(0°<α<180°)得△DEC,点A和点D对应,作EF⊥x轴,DG⊥x轴,垂足分别为F点和G点.(1)当∠α=30°时,求D、E两点的坐标;
(2)当∠α为何值时,△DEC、△EFC和△DCG都相似;
(3)在旋转过程中,若抛物线经过D、E、C三点,请求出一条以y轴为对称轴的抛物线的解析式.
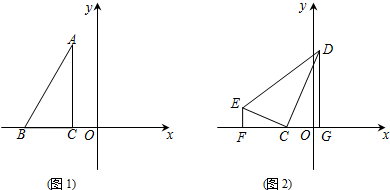
分析 (1)由旋转的性质可知CE=BC=2,∠ECF=30°,进而可求出EF,CF的长,所以点E的坐标可求出;同理即可求出点D的坐标;
(2)若使△DEC、△EFC和△DCG都相似,则旋转角不确定,所以要分四种情况分别讨论:当∠α=30°时,当∠α=60°时,当∠α=120°时,当∠α=150°时;
(3)由(2)②可知,当∠α=60°时,点 E、D关于y轴对称,此时抛物线的对称轴为y轴,易求E(-2,$\sqrt{3}$)、D(2,$\sqrt{3}$),设y=ax2+c,代入C (-1,0)、D(2,$\sqrt{3}$),求出a和c的值即可得到抛物线解析式.
解答 解:(1)∵点A、B、C三点的坐标分别为A (-1,2$\sqrt{3}$),B (-3,0),C (-1,0),
∵AC=2$\sqrt{3}$,BC=2,
∵将△ABC绕点C顺时针旋转∠α=30°得△DEC,点A和点D对应,
∴CE=BC=2,∠ECF=30°,
∴EF=$\frac{1}{2}$CE=1,FC=$\sqrt{3}$,
∴FC=1+$\sqrt{3}$
∴E(-1-$\sqrt{3}$,1),
同理可得:点D(-1+$\sqrt{3}$,3);
(2)①如图2,当∠α=30°时,△DEC、△EFC和△DCG都相似.
理由如下:
∵A(-1,2$\sqrt{3}$),B(-3,0),C(-1,0),
∴BC=2,AC=2$\sqrt{3}$,∠ACB=90°,
∴AB=4,
∴sinA=$\frac{1}{2}$,
∴∠A=30°,∠ABC=60°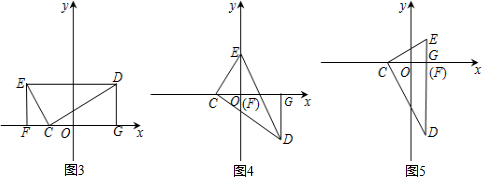 ,
,
∴△DEC中,∠EDC=30°,∠DEC=60°,∠ECD=90°,
∵∠ECF=30°,∠ECD=90°,
∴∠DCG=60°,
∴∠CDG=30°,
∴在△DEC、△EFC和△DCG中:∠EDC=∠ECF=∠CDG=30°,
∠ECD=∠EFC=∠CGD=90°,
∴△DEC∽△CEF∽△DCG.
同理可得以下三种情况:
②如图3,当∠α=60°时,△DEC∽△ECF∽△CDG;
③如图4,当∠α=120°时,△DEC∽△ECF∽△CDG;
④如图5,当∠α=150°时,△DEC∽△CEF∽△DCG.
(3)由(2)②可知,当∠α=60°时,点 E、D关于y轴对称,此时抛物线的对称轴为y轴.
易求:E(-2,$\sqrt{3}$)、D(2,$\sqrt{3}$),
设y=ax2+c,代入C (-1,0)、D(2,$\sqrt{3}$),得$\left\{\begin{array}{l}a+c=0\\ 4a+c=\sqrt{3}\end{array}\right.$,
解得:$\left\{\begin{array}{l}a=\frac{{\sqrt{3}}}{3}\\ c=-\frac{{\sqrt{3}}}{3}\end{array}\right.$,
∴抛物线的解析式为:y=$\frac{{\sqrt{3}}}{3}$x2-$\frac{{\sqrt{3}}}{3}$.
点评 本题考查了二次函数的综合题,用到的知识点有旋转的性质、勾股定理的运用、特殊角的锐角三角函数值、相似三角形的判定和性质、利用待定系数法求二次函数的解析式,此题的难点在(2)小问,解题的关键是运用分类讨论的数学方法,做到对问题的答案不重不漏.

 津桥教育计算小状元系列答案
津桥教育计算小状元系列答案| A. | a+a-1=0 | B. | ($\sqrt{2}$+1)(1-$\sqrt{2}$)=1 | C. | (xy)-1($\frac{1}{2}$xy)2=$\frac{1}{4}$xy | D. | -(-a)4÷a2=a2 |
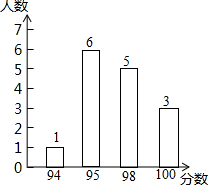 某次比赛中,15名选手的成绩如图所示,则这15名选手成绩的众数和中位数分别是( )
某次比赛中,15名选手的成绩如图所示,则这15名选手成绩的众数和中位数分别是( )| A. | 98,95 | B. | 98,98 | C. | 95,98 | D. | 95,95 |
| A. | 平行四边形 | B. | 圆 | C. | 正五边形 | D. | 等腰三角形 |
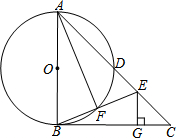 如图,AB为⊙O的直径,BC切⊙O于点B,AC交⊙O于点D,∠BAC=2∠CBE,交AC于点E,交⊙O于点F,连接AF.
如图,AB为⊙O的直径,BC切⊙O于点B,AC交⊙O于点D,∠BAC=2∠CBE,交AC于点E,交⊙O于点F,连接AF.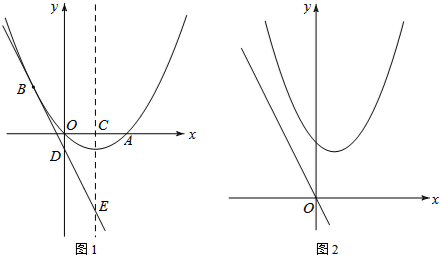
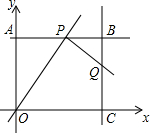 如图,在平面直角坐标系中,四边形OABC为矩形,点A、点C分别在y轴、x轴的正半轴上,OA,OC的长分别是方程x2-7x+12=0的两根(OA<OC).P为直线AB上一动点,直线PQ⊥OP交直线BC于点Q.
如图,在平面直角坐标系中,四边形OABC为矩形,点A、点C分别在y轴、x轴的正半轴上,OA,OC的长分别是方程x2-7x+12=0的两根(OA<OC).P为直线AB上一动点,直线PQ⊥OP交直线BC于点Q.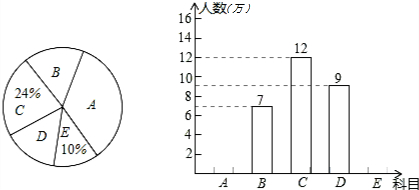 园;D:明月岛,E:青年林场.市旅游局对某月进入景点的人数情况进行调查统计,制成了两幅不完整的统计图(如图).
园;D:明月岛,E:青年林场.市旅游局对某月进入景点的人数情况进行调查统计,制成了两幅不完整的统计图(如图).