题目内容
一个等腰三角形的两边长分别是3和7，则它的周长为（ ）
| A、17 | B、15 |
| C、13 | D、13或17 |
考点：等腰三角形的性质,三角形三边关系
专题：分类讨论
分析：由于未说明两边哪个是腰哪个是底，故需分：（1）当等腰三角形的腰为3；（2）当等腰三角形的腰为7；两种情况讨论，从而得到其周长．
解答：解：①当等腰三角形的腰为3，底为7时，3+3＜7不能构成三角形；
②当等腰三角形的腰为7，底为3时，周长为3+7+7=17．
故这个等腰三角形的周长是17．
故选：A．
②当等腰三角形的腰为7，底为3时，周长为3+7+7=17．
故这个等腰三角形的周长是17．
故选：A．
点评：本题考查的是等腰三角形的性质，在解答此题时要注意进行分类讨论．
练习册系列答案
相关题目
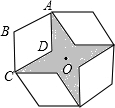如图，是将菱形ABCD以点O为中心按顺时针方向分别旋转90°，180°，270°后形成的图形．若∠BAD=60°，AB=2，则图中阴影部分的面积为
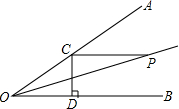如图，∠AOB=30°，P是∠AOB的平分线上一点，PC∥OB，交OA于C，CD⊥OB于D．若PC=3，则CD的长为若α，β是方程x2-2x-3=0的两个实数根，则α2+β2的值为（ ）
| A、10 | B、9 | C、7 | D、5 |
如图，已知：△ABC中，AB=AC，M是BC的中点，D、E分别是AB、AC边上的点，且BD=CE．求证：MD=ME．
如图，一艘轮船以30海里/小时的速度由西向东航行，途中接到台风警报，台风中心正以60海里/小时的速度由南向北移动，距台风中心20海里的圆形区域（包括边界）都属于台风区，当轮船到A处时，测得台风中心移到位于点A正南方向的B处，且AB=40海里．