题目内容
如图,直角三角形纸片ABC中,AB=3,AC=4,D为斜边BC中点,第1次将纸片折叠,使点A与点D重合,折痕与
AD交与点P1;设P1D的中点为D1,第2次将纸片折叠,使点A与点D1重合,折痕与AD交于点P2;设P2D1的中点为D2,第3次将纸片折叠,使点A与点D2重合,折痕与AD交于点P3;…;设Pn-1Dn-2的中点为Dn-1,第n次将纸片折叠,使点A与点Dn-1重合,折痕与AD交于点Pn(n>2),则AP6的长为( )

AD交与点P1;设P1D的中点为D1,第2次将纸片折叠,使点A与点D1重合,折痕与AD交于点P2;设P2D1的中点为D2,第3次将纸片折叠,使点A与点D2重合,折痕与AD交于点P3;…;设Pn-1Dn-2的中点为Dn-1,第n次将纸片折叠,使点A与点Dn-1重合,折痕与AD交于点Pn(n>2),则AP6的长为( )

A、
| ||
B、
| ||
C、
| ||
D、
|
考点:翻折变换(折叠问题)
专题:
分析:根据题意,分别求出AP1、AP2、AP3的长度,经猜想、验证,即可解决问题.
解答: 解:由题意得:
解:由题意得:
∵△ABC为直角三角形,
且AC=3,AB=3,
∴BC=5;而AD为斜边的中线,
∴AD=
;
第一次折叠:AP1=
×
=
;
第2次折叠:AP2
=(
+
)×
=
;
第3次折叠:AP3
=
,
∴可以猜测:第n次折叠,APn
=
,
∴AP6=
.
故选D.
 解:由题意得:
解:由题意得:∵△ABC为直角三角形,
且AC=3,AB=3,
∴BC=5;而AD为斜边的中线,
∴AD=
| 5 |
| 2 |
第一次折叠:AP1=
| 5 |
| 2 |
| 1 |
| 2 |
=
| 5 |
| 4 |
第2次折叠:AP2
=(
| 5 |
| 4 |
| 5 |
| 8 |
| 1 |
| 2 |
| 15 |
| 16 |
第3次折叠:AP3
=
| 45 |
| 64 |
∴可以猜测:第n次折叠,APn
=
| 5×3n-1 |
| 4×4n-1 |
∴AP6=
| 5×35 |
| 212 |
故选D.
点评:该题主要考查了翻折变换的性质及其应用、勾股定理、直角三角形的性质等知识点问题;解题的关键是灵活运用翻折变换的性质等知识点;对猜想、判断能力也提出了一定的要求.

练习册系列答案
相关题目
下列图中,∠1和∠2是对顶角的是( )
A、 |
B、 |
C、 |
D、 |

 已知:如图,点A、E、F、C在同一直线上,AD∥BC,AD=CB,AE=CF.求证:∠B=∠D.
已知:如图,点A、E、F、C在同一直线上,AD∥BC,AD=CB,AE=CF.求证:∠B=∠D. 如图,直角三角形纸片ABC中,∠C=90°,AC=6,BC=8,将纸片沿AD折叠,使C点与AB边上的点E重合.
如图,直角三角形纸片ABC中,∠C=90°,AC=6,BC=8,将纸片沿AD折叠,使C点与AB边上的点E重合. 实数a,b,c在数轴上的位置如图,请化简:|c|-
实数a,b,c在数轴上的位置如图,请化简:|c|-
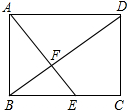 如图,四边形ABCD是矩形,点E在BC边上,AE与BD交于点F,∠BAE=∠ADB.
如图,四边形ABCD是矩形,点E在BC边上,AE与BD交于点F,∠BAE=∠ADB.