题目内容
3.若关于x的函数y=(a-2)x2-(2a-1)x+a的图象与坐标轴只有两个公共点,则a的值为2,0,$-\frac{1}{4}$.分析 根据函数图象与坐标轴有两个公共点,即与x轴一个交点,与y轴有一个交点;根据不同的情况分析,求出a的值即可.
解答 解:因为关于x的函数y=(a-2)x2-(2a-1)x+a的图象与坐标轴只有两个交点,
若与x轴、y轴各有一个交点,
∴此函数若为二次函数,则b2-4ac=[-(2a-1)]2-4(a-2)a=4a+1=0,解得:a=-$\frac{1}{4}$,
若a=0,二次函数图象过原点,满足题意,
若此函数为一次函数,则a-2=0,所以a=2.
所以若关于x的函数y=(a-2)x2-2(2a-1)x+a的图象与坐标轴只有两个交点,则a=2、0、-$\frac{1}{4}$.
故答案为:2,0,-$\frac{1}{4}$.
点评 本题主要考查了函数图象与坐标轴的交点,解决此题的关键是能从不同的角度分析求解,解决此题需要考虑全面.

练习册系列答案
相关题目
8.下列关于近似数的说法,正确的是( )
| A. | 3.10精确到十分位 | B. | 1.6×105精确到万位 | ||
| C. | 300精确到百位 | D. | 近似数1.7和1.70表示同一个数 |
15.下列计算正确的是( )
| A. | a4÷b4=a | B. | 3x2+4x2=7x4 | C. | (-a2)3=a6 | D. | a3•(-a)2=a5 |
12.某商品经过连续两次降价,销售单价由原来的125元降到80元.设平均每次降价的百分率为x,由题意列方程:( )
| A. | 125(1-x)2=80 | B. | 125(1-2x)=80 | C. | 125(1-2x)2=80 | D. | 80(1-x)2=125 |
13.小明利用计算机设计了一个计算程序,输入和输出的数据如表:
那么,当输入数据为201时,输出的数据为605.
| 输入 | … | 1 | 2 | 3 | 4 | 5 | … |
| 输出 | … | 5 | 8 | 11 | 14 | 17 | … |
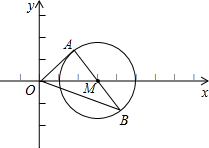 如图,平面直角坐标系xOy中,M点的坐标为(3,0),⊙M的半径为2,过M点的直线与⊙M的交点分别为A、B,则△AOB的面积的最大值为6.
如图,平面直角坐标系xOy中,M点的坐标为(3,0),⊙M的半径为2,过M点的直线与⊙M的交点分别为A、B,则△AOB的面积的最大值为6.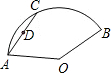 扇形AOB中,∠AOB=150°,AC=AO=6,D为AC的中点,当弦AC沿扇形运动时,点D所经过的路程为$\frac{3\sqrt{3}π}{2}$.
扇形AOB中,∠AOB=150°,AC=AO=6,D为AC的中点,当弦AC沿扇形运动时,点D所经过的路程为$\frac{3\sqrt{3}π}{2}$. 已知:如图,AE平分∠BAC,∠BAC=2∠B,AB=2AC.求证:(1)∠C=90°;(2)AE=2CE.
已知:如图,AE平分∠BAC,∠BAC=2∠B,AB=2AC.求证:(1)∠C=90°;(2)AE=2CE.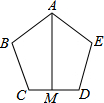 如图,AB=AE,BC=DE,∠B=∠E,AM⊥CD,垂足为点M.求证:CM=DM.
如图,AB=AE,BC=DE,∠B=∠E,AM⊥CD,垂足为点M.求证:CM=DM.