题目内容
11.如果最简二次根式$\sqrt{1+a}$与$\sqrt{2a-1}$是同类根式,那么a=( )| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
分析 根据同类二次根式的定义得出方程1+a=2a-1,求出即可.
解答 解:∵最简二次根式$\sqrt{1+a}$与$\sqrt{2a-1}$是同类根式,
∴1+a=2a-1,
解得:a=2,
故选B.
点评 本题考查同类二次根式的概念,同类二次根式是化为最简二次根式后,被开方数相同的二次根式称为同类二次根式.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
1.下列生活现象中,不是平移现象的是( )
| A. | 站在运行着的电梯上的人 | B. | 左右推动推拉窗 | ||
| C. | 躺在火车上睡觉的旅客 | D. | 正在荡秋千的小明 |
2.三角形两边长为6与8,那么周长l的取值范围( )
| A. | 2<l<14 | B. | 16<l<28 | C. | 14<l<28 | D. | 20<l<24 |
6.下列计算正确的是( )
| A. | $\sqrt{64}$的平方根为±8 | B. | $\sqrt{64}$的算术平方根为8 | ||
| C. | $\sqrt{64}$的立方根为2 | D. | $\sqrt{64}$的立方根为±2 |
20.如果a=-$\frac{1}{4}$,b=-2,c=-2$\frac{3}{\begin{array}{l}4\end{array}}$,那么|a|+|b|-|c|等于( )
| A. | -$\frac{1}{2}$ | B. | 1$\frac{1}{2}$ | C. | $\frac{1}{2}$ | D. | -1$\frac{1}{2}$ |
1.若点A(2,4)在函数y=kx-2的图象上,则下列各点中,也在此函数图象上的是( )
| A. | ($\frac{2}{3}$,0) | B. | (0,3) | C. | (8,20) | D. | (3,6) |
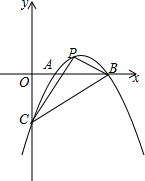 如图,抛物线y=-$\frac{2}{5}$x2+$\frac{12}{5}$x-2与x轴交于A、B,与y轴交于点C,点P为抛物线上一点,且∠PBO=∠CBO,求点P的坐标.
如图,抛物线y=-$\frac{2}{5}$x2+$\frac{12}{5}$x-2与x轴交于A、B,与y轴交于点C,点P为抛物线上一点,且∠PBO=∠CBO,求点P的坐标.