题目内容
2.一组数据x1,x2,…xn的平均数为$\overline{x}$,另一组数据y1,y2,…yn的平均数为$\overline{y}$,则第三组数据x1+y1,x2+y2,…xn+yn的平均数为$\overline{x}$+$\overline{y}$.(用$\overline{x}$,$\overline{y}$表示)分析 平均数的计算方法是求出所有数据的和,然后除以数据的总个数.先求数据x1,x2,x3…xn与数据y1,y2,…yn的和,然后用平均数的定义求新数据的平均数.
解答 解:∵数据x1,x2,…xn的平均数为$\overline{x}$,数据y1,y2,…yn的平均数为$\overline{y}$,
∴x1+x2+x3+…+xn=n$\overline{x}$,y1+y2+…+yn=n$\overline{y}$,
∴数据x1+y1,x2+y2,…xn+yn的平均数为(x1+y1+x2+y2+…+xn+yn)÷n
=(n$\overline{x}$+n$\overline{y}$)÷n
=$\overline{x}$+$\overline{y}$.
故答案为$\overline{x}$+$\overline{y}$.
点评 本题考查的是算术平均数:对于n个数x1,x2,…,xn,则$\overline{x}$=$\frac{1}{n}$(x1+x2+…+xn)就叫做这n个数的算术平均数.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
14.一元二次方程x2-4x+2=0根的判别式的值为( )
| A. | 8 | B. | -8 | C. | 2$\sqrt{2}$ | D. | -2$\sqrt{2}$ |
11.下列命题是假命题的是( )
| A. | 不在同一直线上的三点确定一个圆 | |
| B. | 正六边形的内角和是720° | |
| C. | 矩形的对角线互相垂直且平分 | |
| D. | 角平分线上的点到角两边的距离相等 |
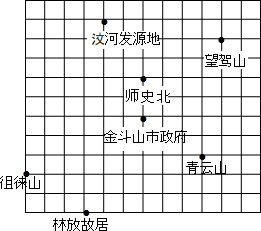 图中是某市旅游景点示意图,请建立适当的坐标系,使横轴与网格线的横线平行,纵轴与网格线的竖线平行,并且使青云山的坐标为(3,-2),然后再写出下列各景点的坐标.
图中是某市旅游景点示意图,请建立适当的坐标系,使横轴与网格线的横线平行,纵轴与网格线的竖线平行,并且使青云山的坐标为(3,-2),然后再写出下列各景点的坐标.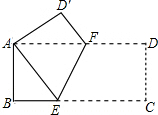 如图,在矩形ABCD中,AB=8,BC=16,将矩形ABCD沿EF折叠,使点C与点A重合,则折痕EC的长为( )
如图,在矩形ABCD中,AB=8,BC=16,将矩形ABCD沿EF折叠,使点C与点A重合,则折痕EC的长为( )