题目内容
2.已知一条直线与y轴交于点A(0,-4),与x轴交于点B(-3,0).(1)在平面直角坐标系中,画出这条直线;
(2)求这条直线的函数表达式;
(3)若点C与点A关于x轴对称,求△ABC的面积与周长.
分析 (1)在平面直角坐标系内描出点(0,-4)和(-3,0),画出一次函数的图象即可;
(2)把点(0,-4)和(-3,0)代入直线y=kx+b求出k、b的值即可得出直线的解析式;
(3)求出C点的坐标,根据勾股定理求得AB,即可BC,从而求得△ABC的面积与周长.
解答 解:(1)其图象如图所示: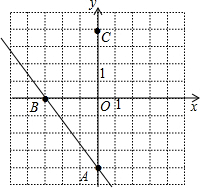
(2)∵直线与y轴交于点A(0,-4),与x轴交于点B(-3,0).
设直线y=kx+b,
∴$\left\{\begin{array}{l}{b=-4}\\{-3k+b=0}\end{array}\right.$,解得$\left\{\begin{array}{l}{k=-\frac{4}{3}}\\{b=-4}\end{array}\right.$,
∴直线的解析式为:y=$\frac{4}{3}$x-4;
(3)∵A(0,-4),B(-3,0),
∴AB=$\sqrt{{3}^{2}+{4}^{2}}$=5,
∵点C与点A关于x轴对称,
∴C(0,4),
∴AC=4+4=8,BC=AB=5,
∴△ABC的面积=$\frac{1}{2}$AC•OB=$\frac{1}{2}×8×3$=12,
△ABC的周长=5+5+8=18.
点评 本题考查的是用待定系数法求一次函数的解析式及一次函数的性质,熟知用待定系数法求一次函数的解析式的基本步骤是解答此题的关键.

练习册系列答案
 阳光课堂课时作业系列答案
阳光课堂课时作业系列答案
相关题目
20. 如图,已知∠ACB是⊙O的圆周角,∠ACB=35°,则圆心角∠AOB是( )
如图,已知∠ACB是⊙O的圆周角,∠ACB=35°,则圆心角∠AOB是( )
 如图,已知∠ACB是⊙O的圆周角,∠ACB=35°,则圆心角∠AOB是( )
如图,已知∠ACB是⊙O的圆周角,∠ACB=35°,则圆心角∠AOB是( )| A. | 17.5° | B. | 35° | C. | 50° | D. | 70° |
1. 分别以直角三角形的三边为一边向外作正方形A、B、C的面积如图所示,则字母A所代表的正方形的面积为( )
分别以直角三角形的三边为一边向外作正方形A、B、C的面积如图所示,则字母A所代表的正方形的面积为( )
 分别以直角三角形的三边为一边向外作正方形A、B、C的面积如图所示,则字母A所代表的正方形的面积为( )
分别以直角三角形的三边为一边向外作正方形A、B、C的面积如图所示,则字母A所代表的正方形的面积为( )| A. | 16 | B. | 12 | C. | 4 | D. | 2 |
18.下列式子合并同类项正确的是( )
| A. | 3x+5y=8xy | B. | 15ab-15ba=0 | C. | 3y2-y2=3 | D. | 7x3-6x2=x |
5.在抛物线y=x2-6x+c上有三个点,A(-1,y1),B(2,y2),C(3+$\sqrt{2}$,y3)三点,则y1,y2,y3的大小关系是( )
| A. | y1>y2>y3 | B. | y1<y2<y3 | C. | y1>y3>y2 | D. | 不确定 |
11.用配方法解一元二次方程x2-6x+5=0,此方程可化为( )
| A. | (x-3)2=4 | B. | (x-3)2=14 | C. | (x+3)2=4 | D. | (x+3)2=14 |
 如图,某计算机中有
如图,某计算机中有 、
、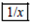 、
、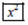 三个按键,以下是这三个按键的功能.
三个按键,以下是这三个按键的功能.