题目内容
18.已知a-b=5,且c-b=10,则a2+b2+c2-ab-bc-ac等于75.分析 由已知a-b=5,且c-b=10,两等式左右两边分别相减,可得到a-c=-5,观察a2+b2+c2-ab-bc-ac发现,利用完全平方差公式,可转化为$\frac{1}{2}$[(a-b)2+(b-c)2+(a-c)2],再将上面的式子代入,问题得解.
解答 解:∵a-b=5,c-b=10
∴a-c=-5
a2+b2+c2-ab-bc-ac=$\frac{1}{2}$[(a-b)2+(b-c)2+(a-c)2]=$\frac{1}{2}$×[52+(-10)2+(-5)2]=75.
故答案为:75.
点评 本题主要考查完全平方差公式因式分解.将a2+b2+c2-ab-bc-ac看做$\frac{1}{2}$[(a-b)2+(b-c)2+(a-c)2]是难点.

练习册系列答案
相关题目
8.“元旦”期间,某文具店购进100只两种型号的文具进行销售,其进价和售价如下表:
(1)该店用1300元可以购进A,B两种型号的文具各多少只?
(2)若把所购进A,B两种型号的文具全部销售完,利润率超过40%没有?请你说明理由.
| 型号 | 进价(元/只) | 售价(元/只) |
| A型 | 10 | 12 |
| B型 | 15 | 23 |
(2)若把所购进A,B两种型号的文具全部销售完,利润率超过40%没有?请你说明理由.
3. 如图,∠AOP=∠BOP,CP∥OB,CP=3,则OC=( )
如图,∠AOP=∠BOP,CP∥OB,CP=3,则OC=( )
 如图,∠AOP=∠BOP,CP∥OB,CP=3,则OC=( )
如图,∠AOP=∠BOP,CP∥OB,CP=3,则OC=( )| A. | 2 | B. | 3 | C. | 4 | D. | 5 |
10.如果a-b=4,ab=7,那么a2b-ab2的值是( )
| A. | -28 | B. | -11 | C. | 28 | D. | 11 |
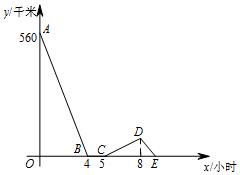 一辆慢车与一辆快车分别从甲、乙两地同时出发,匀速相向而行,两车在途中相遇后都停留在一段时间,然后分别按原速一同驶往甲地后停车.设慢车行驶的时间为x小时,两车之间的距离为y千米,图中折线表示x与y之间的关系,
一辆慢车与一辆快车分别从甲、乙两地同时出发,匀速相向而行,两车在途中相遇后都停留在一段时间,然后分别按原速一同驶往甲地后停车.设慢车行驶的时间为x小时,两车之间的距离为y千米,图中折线表示x与y之间的关系,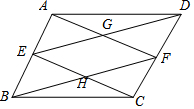 在平行四边形ABCD中,E、F分别是AB、CD的中点,AF与DE相交于点G,GE与BF相交于点H.
在平行四边形ABCD中,E、F分别是AB、CD的中点,AF与DE相交于点G,GE与BF相交于点H.