题目内容
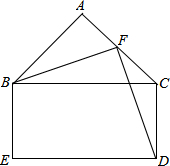 如图,在△ABC中,∠A=90°,AB=AC,F为AC边上中点,四边形BEDC是矩形,且BC=2BE,求证:△FBD是等腰三角形.
如图,在△ABC中,∠A=90°,AB=AC,F为AC边上中点,四边形BEDC是矩形,且BC=2BE,求证:△FBD是等腰三角形.考点:全等三角形的判定与性质,等腰直角三角形
专题:证明题
分析:首先证明△ABF∽△CBD,可得∠BAF=∠CBD,进而得到∠FBD=∠FBC+∠CBD=∠ABC=45°,根据相似三角形的性质可得
=
=
,作DG垂直于BF于G,再证明F、G重合即可.
| FB |
| DB |
| AB |
| CB |
| ||
| 2 |
解答: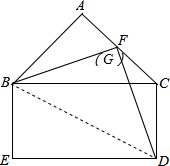 证明:∵∠A=90°,AB=AC,
证明:∵∠A=90°,AB=AC,
∴BC=
AB,
∵F为AC边上中点,
∴AF=
AC=
AB,
∵BC=2BE,
∴
=
=2,
∵∠A=∠BCD=90°,
∴△ABF∽△CBD,
∴∠BAF=∠CBD,
∴∠FBD=∠FBC+∠CBD=∠ABC=45°,
∵
=
=
,
作DG垂直于BF于G,
∴
=
,
∴F、G重合,
∴∠BFD=90°,
∴△FBD是直角等腰三角形.
 证明:∵∠A=90°,AB=AC,
证明:∵∠A=90°,AB=AC,∴BC=
| 2 |
∵F为AC边上中点,
∴AF=
| 1 |
| 2 |
| 1 |
| 2 |
∵BC=2BE,
∴
| AB |
| AF |
| BC |
| CD |
∵∠A=∠BCD=90°,
∴△ABF∽△CBD,
∴∠BAF=∠CBD,
∴∠FBD=∠FBC+∠CBD=∠ABC=45°,
∵
| FB |
| DB |
| AB |
| CB |
| ||
| 2 |
作DG垂直于BF于G,
∴
| GB |
| DB |
| ||
| 2 |
∴F、G重合,
∴∠BFD=90°,
∴△FBD是直角等腰三角形.
点评:此题主要考查了相似三角形的判定与性质,以及直角三角形的判定,关键是正确证明△ABF∽△CBD.

练习册系列答案
相关题目
 如图,菱形ABCD中,对角线BD=3,∠BAD=60°,则AC的长为( )
如图,菱形ABCD中,对角线BD=3,∠BAD=60°,则AC的长为( )A、2
| ||
B、3
| ||
C、4
| ||
| D、6 |
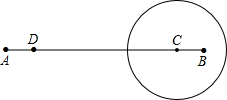 如图,线段AB=8cm,点D从A点出发沿AB向B点匀速运动,速度为1cm/s,同时点C 从B点出发沿BA向A点以相同速度运动,以点C为圆心,2cm长为半径作⊙C,点D到达B点时⊙C也停止运动,设运动时间为t秒,则点D在⊙C内部时t的取值范围是
如图,线段AB=8cm,点D从A点出发沿AB向B点匀速运动,速度为1cm/s,同时点C 从B点出发沿BA向A点以相同速度运动,以点C为圆心,2cm长为半径作⊙C,点D到达B点时⊙C也停止运动,设运动时间为t秒,则点D在⊙C内部时t的取值范围是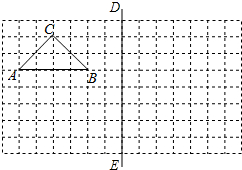 如图,在所给网格图(每小格均为边长是1的正方形)中完成下列各题:
如图,在所给网格图(每小格均为边长是1的正方形)中完成下列各题: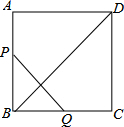 如图,在矩形ABCD中,∠C=90°,AB=6cm,BC=8cm,点P、Q分别是AB、BC边上的动点.若点P以1cm/s的速度从A出发向点B运动,点Q以2cm/s的速度从点B出发向点C运动,且两点同时出发,问:出发时间为多少秒时△BCD与△PBQ相似?
如图,在矩形ABCD中,∠C=90°,AB=6cm,BC=8cm,点P、Q分别是AB、BC边上的动点.若点P以1cm/s的速度从A出发向点B运动,点Q以2cm/s的速度从点B出发向点C运动,且两点同时出发,问:出发时间为多少秒时△BCD与△PBQ相似?