题目内容
在四边形ABCD中，AB∥CD，AD=BC，∠B=90°，求证：四边形ABCD是矩形．
考点：矩形的判定
专题：证明题
分析：可利用反证法来证明，假设不是矩形，可得出AD≠BC，得证．
解答：证明：假设四边形ABCD不是矩形，
则∠ADC≠∠DAB，即∠ADC和∠DAB均不为直角，
∵AB∥CD，∠B=90°，
∴∠C+∠B=180°，
∴∠C=∠B=90°，
∴BC为AB和CD之间的距离，
∵∠ADC和∠DAB均不为直角，
∴AD不是AB和CD两平行线间的距离，
∴AD≠BC，
这与已知AD=BC矛盾，
∴假设不成立，
∴四边形ABCD为矩形．
则∠ADC≠∠DAB，即∠ADC和∠DAB均不为直角，
∵AB∥CD，∠B=90°，
∴∠C+∠B=180°，
∴∠C=∠B=90°，
∴BC为AB和CD之间的距离，
∵∠ADC和∠DAB均不为直角，
∴AD不是AB和CD两平行线间的距离，
∴AD≠BC，
这与已知AD=BC矛盾，
∴假设不成立，
∴四边形ABCD为矩形．
点评：本题主要考查矩形的判定方法，当直接证明结论不好证明时可以用间接证明，即可以利用反证法来证明．
练习册系列答案
相关题目
等边△ABC在数轴上的位置如图所示，点A、C对应的数分别为0和-1，若△ABC绕顶点沿顺时针方向在数轴上连续翻转，翻转1次后，点B所对应的数为1，则连续翻转2015次后，点A（ ）
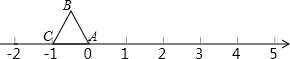
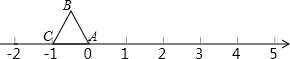
| A、不对应任何数 |
| B、对应的数是2013 |
| C、对应的数是2014 |
| D、对应的数是2015 |
如图，菱形ABCD中，对角线BD=3，∠BAD=60°，则AC的长为（ ）A、2
| ||
B、3
| ||
C、4
| ||
| D、6 |
