题目内容
19.如图1,在矩形ABCD中,动点P从点A出发,沿A→D→C→B的路径运动.设点P运动的路程为x,△PAB的面积为y.图2反映的是点P在A→D→C运动过程中,y与x的函数关系.请根据图象回答以下问题:(1)矩形ABCD的边AD=2,AB=4;
(2)写出点P在C→B运动过程中y与x的函数关系式,并在图2中补全函数图象.

分析 (1)根据题意,结合图形确定出矩形ABCD的边AD与AB即可;
(2)根据题意表示出PB的长,由AB为底,PB为高,表示出三角形APB面积,确定出y与x的函数关系式,作出相应的图象,如图2所示.
解答 解:(1)根据题意得:矩形ABCD的边AD=2,AB=4;
故答案为:2;4;
(2)当点P在C→B运动过程中,PB=8-x,
∴y=S△APB=$\frac{1}{2}$×4×(8-x),即y=-2x+16(6≤x≤8),
正确作出图象,如图所示:
点评 此题属于四边形综合题,涉及的知识有:矩形的性质,三角形的面积,函数及其图象,弄清题中动点P的运动轨迹是解本题的关键.

练习册系列答案
 数学奥赛暑假天天练南京大学出版社系列答案
数学奥赛暑假天天练南京大学出版社系列答案
相关题目
10.等腰三角形的顶角为100°,则它的一个底角是( )
| A. | 40° | B. | 50° | C. | 60° | D. | 80° |
4.如果不等式$\left\{\begin{array}{l}{x<5}\\{x>m}\end{array}\right.$无解,那么m的取值范围是( )
| A. | m<5 | B. | m≤5 | C. | m>5 | D. | m≥5 |
11. 如图,在Rt△ABC中,AC=6,BC=4,将△ABC绕直角顶点C顺时针旋转90°得到△DEC,若点F是DE的中点,连接AF,则AF的长为( )
如图,在Rt△ABC中,AC=6,BC=4,将△ABC绕直角顶点C顺时针旋转90°得到△DEC,若点F是DE的中点,连接AF,则AF的长为( )
 如图,在Rt△ABC中,AC=6,BC=4,将△ABC绕直角顶点C顺时针旋转90°得到△DEC,若点F是DE的中点,连接AF,则AF的长为( )
如图,在Rt△ABC中,AC=6,BC=4,将△ABC绕直角顶点C顺时针旋转90°得到△DEC,若点F是DE的中点,连接AF,则AF的长为( )| A. | 3 | B. | 4 | C. | 5 | D. | 4$\sqrt{2}$ |
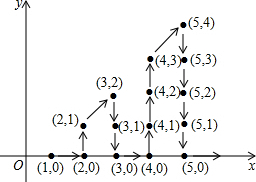 如图,在平面直角坐标系中,有若干个整数点,其顺序按图中“→”方向排列,如(1,0),(2,0),(2,1),(3,2),(3,1),(3,0)根据这个规律探索可得,第2016个点的横坐标为63.
如图,在平面直角坐标系中,有若干个整数点,其顺序按图中“→”方向排列,如(1,0),(2,0),(2,1),(3,2),(3,1),(3,0)根据这个规律探索可得,第2016个点的横坐标为63. 如图,一次函数$y=\frac{1}{2}x$的图象与反比例函数$y=\frac{k}{x}(k>0)$的图象交于A、B两点,AC⊥y轴,且S△AOC=16.
如图,一次函数$y=\frac{1}{2}x$的图象与反比例函数$y=\frac{k}{x}(k>0)$的图象交于A、B两点,AC⊥y轴,且S△AOC=16.