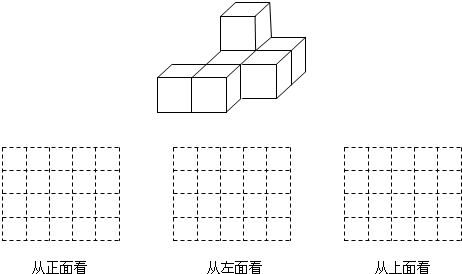
题目内容
在△ABC中,∠C=90°.
(1)若∠B=30°,AB=6,求BC的长.
(2)若AC:BC=3:4,AB=10,求AC、BC的长.
(1)若∠B=30°,AB=6,求BC的长.
(2)若AC:BC=3:4,AB=10,求AC、BC的长.
考点:勾股定理,含30度角的直角三角形
专题:
分析:(1)根据题意画出图形,先根据∠B=30°,AB=6求出AC的长,再根据勾股定理求出BC的长即可;
(2)设AC=3x,则BC=4x,根据勾股定理求出x的值,进而可得出结论.
(2)设AC=3x,则BC=4x,根据勾股定理求出x的值,进而可得出结论.
解答: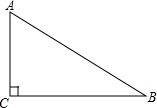 解:(1)如图所示,
解:(1)如图所示,
∵∠C=90°,∠B=30°,AB=6,
∴AC=
AB=3,
∴BC=
=
=3
;
(2)∵∠C=90°,AC:BC=3:4,AB=10,
∴设AC=3x,则BC=4x.
∵AC2+BC2=AB2,即(3x)2+(4x)2=102,解得x=2,
∴AC=6,BC=4.
 解:(1)如图所示,
解:(1)如图所示,∵∠C=90°,∠B=30°,AB=6,
∴AC=
| 1 |
| 2 |
∴BC=
| AB2-AC2 |
| 62-32 |
| 3 |
(2)∵∠C=90°,AC:BC=3:4,AB=10,
∴设AC=3x,则BC=4x.
∵AC2+BC2=AB2,即(3x)2+(4x)2=102,解得x=2,
∴AC=6,BC=4.
点评:本题考查的是勾股定理,熟知在任何一个直角三角形中,两条直角边长的平方之和一定等于斜边长的平方是解答此题的关键.

练习册系列答案
 中考解读考点精练系列答案
中考解读考点精练系列答案
相关题目
已知B是线段AC上的一点,且BC=
AB,D是AC的中点,若DC=2cm,则AB的长为( )
| 1 |
| 3 |
| A、4cm | ||
| B、3cm | ||
| C、2cm | ||
D、
|
 如图,已知△ABC中,∠C=90°,AC=BC=
如图,已知△ABC中,∠C=90°,AC=BC=| 2 |
| A、15° | B、20° |
| C、30° | D、45° |
观察下列多项式,是完全平方式的是( )
| A、x2-4x+2 |
| B、x2+x+1 |
| C、x2-4x-4 |
| D、4x2+4x+1 |
 如图,动点P从(0,3)出发,沿所示方向运动,每当碰到矩形的边时反弹.反弹时反射角等于入射角,当点P第2015次碰到矩形的边时,点P的坐标为( )
如图,动点P从(0,3)出发,沿所示方向运动,每当碰到矩形的边时反弹.反弹时反射角等于入射角,当点P第2015次碰到矩形的边时,点P的坐标为( )| A、(1,4) |
| B、(5,0) |
| C、(6,4) |
| D、(8,3) |