Question

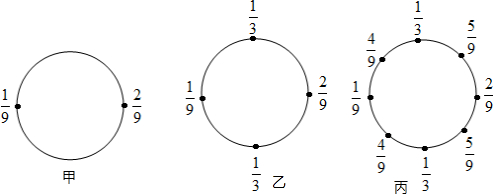
11．如图所示，每个圆周上的数是按下述规则逐次标出的：第一次先在圆周上标出$\frac{1}{9}$，$\frac{2}{9}$两个数（如图甲），第二次又在第一次标出的两个数之间的圆周上，分别标出这两个数的和（如图乙），第三次再在第二次标出的所有相邻数之间的圆周上，分别标出这相邻两数的和（如图丙）；按照此规则，依此类推，一直标下去．
（1）设n是大于1的自然数，第n-1次标完数字后，圆周上所有数字的和记为S_n-1；第n次标完数字后，圆周上所有数字的和记为S_n，猜想并写出S_n与S_n-1的等量关系；
（2）请你求出S₁₀₂的值．

Answer 1

分析 （1）当n=1时，S=$\frac{3}{9}$，当n=2时，S=$\frac{9}{9}$，当n=3时，S=$\frac{27}{9}$，由此可知每次标完数字后的和是前一次标完数字后的和的3倍，即可推出S_n与S_n-1的关系；
（2）根据（1）所推出的结论可知，第n次标完后，S_n=3^n-2，所以S₁₀₂的值为3¹⁰⁰．

解答 解：（1）∵当n=1时，S₁=$\frac{3}{9}$，
当n=2时，S₂=$\frac{9}{9}$，
当n=3时，S₃=$\frac{27}{9}$，
∴3S₁=S₂，3S₂=S₃，S_n=3^n-2，
∴S_n=3S_n-1，
（2）∵S_n=3^n-2，
∴S₁₀₂=3¹⁰⁰．

点评 此题考查数字的变化规律，关键在于通过计算每次标注完数字后的和，得出一般的计算方法解决问题．