题目内容
12.先化简再求值:$(\frac{3}{x-1}-x-1)÷\frac{x-2}{{{x^2}-2x+1}}$,其中x是方程x2=2x的根.分析 先根据分式混合运算的法则把原式进行化简,再求出x的值代入进行计算即可.
解答 解:原式=$\frac{3-(x+1)(x-1)}{x-1}$•$\frac{(x-1)^{2}}{x-2}$
=$\frac{3-{x}^{2}+1}{x-1}$•$\frac{{(x-1)}^{2}}{x-2}$
=$\frac{-(x+2)(x-2)}{x-1}$•$\frac{{(x-1)}^{2}}{x-2}$
=(-x-2)•(x-1),
∵解方程x2=2x得x1=0,x2=2(舍去),
∴当x=0时,原式=(-0-2)•(0-1)=2.
点评 本题考查的是分式的化简求值,熟知分式混合运算的法则是解答此题的关键.

练习册系列答案
相关题目
17.Rt△ABC中,如果斜边上的中线CD=5cm,那么斜边AB为( )cm.
| A. | 5 | B. | 12 | C. | 6 | D. | 10 |
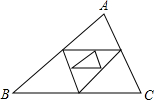 已知△ABC周长为1,连结△ABC三边中点构成第二个三角形,再连结第二个三角形三边中点构成第三个三角形,以此类推,第2014个三角形的周长为($\frac{1}{2}$)2013.
已知△ABC周长为1,连结△ABC三边中点构成第二个三角形,再连结第二个三角形三边中点构成第三个三角形,以此类推,第2014个三角形的周长为($\frac{1}{2}$)2013.