��Ŀ����
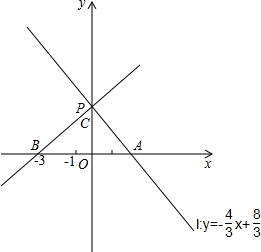 ��ƽ��ֱ������ϵ�У���O��ԭ�㣮ֱ��l��y=-
��ƽ��ֱ������ϵ�У���O��ԭ�㣮ֱ��l��y=-| 4 |
| 3 |
| 8 |
| 3 |
��1����ֱ����y��Ľ���P��������߶�BC�ij��ȣ�
��2��?����CD=1�����D�����ꣻ?
�ڹ���D��ֱ��m��l����x���ڵ�E������CE������D���߶�CB���˶�ʱ�����ʹ��������CDE��������ʱ��D��λ�ã�?
����ֱ��CB���Ƿ���ڵ�Dʹ������CDE���������
| 9 |
| 2 |
���㣺һ�κ����ۺ���
ר�⣺
��������1����x=0�����y��ֵ�������P�����꣬���ݡ�ABC����APO�������BC�ij���
��2������ֱ��l�Ľ���ʽ���ֱ��BC��б�ʣ�����б�ʼ������
=
��?
=
��
=
��Ȼ���ٸ���BD�ij��������DE��BE���������OE���Ӷ����D�����ꣻ�������ۣ�����D�ڵ�C��ߣ�����D�ڵ�C�ұ����������⣻
��3���������ۼ�����ã�
��2������ֱ��l�Ľ���ʽ���ֱ��BC��б�ʣ�����б�ʼ������
| OC |
| OB |
| 3 |
| 4 |
| BE |
| BD |
| 4 |
| 5 |
| DE |
| BD |
| 3 |
| 5 |
��3���������ۼ�����ã�
����⣺��1����x=0����y=
��
��ֱ����y��Ľ���P��0��
����
�ߡ�ACB=��POA=90�㣬��BAC=��PAO��
���ABC����APO��
��
=
��
��ֱ��l��y=-
x+
��x�ύ�ڵ�A������B��-3��0����
��A��2��0����
��OP=
��OA=2��AB=5��
��AP=
=
��
��
=
��
��BC=4��

��2���������ۣ�
����D�ڵ�C��ߣ�
��CD=1��BC=4��
��BD1=3��
��BC��l��ֱ��l��y=-
x+
��
��ֱ��BC��б��Ϊ
��
��
=
��
��sin��OBC=
��cos��OBC=
��
��cos��OBC=
=
��sin��OBC=
=
��
��BE1=
��D1E1=
��
��OE1=OB-BE1=
��
��D1(-
��
)��
����D�ڵ�C�ұߣ���BD2=5��ͬ����֤sin��OBC=
=
��cos��OBC=
=
��
����D2 E2=3��BE2=4��
��OE2=4-3=1��
��D2 ��1��3����
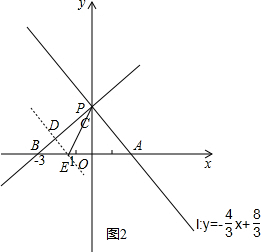
����ͼ2��ʾ����CD=a����BD=4-a��
��m��l��BC��l
��BC��m
���BDE��ֱ�������Σ�
��tan��DBE=
��
��DE=
BD=
��4-a����
��S��CDE=
•
��4-a��a=-
��a-2��2+
��
�൱a=2ʱ��CDE��������
��ʱD��-
��
����
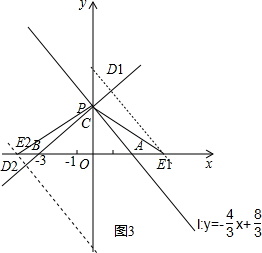
����ͼ3��ʾ
��D���߶�BC��ʱ�����ڡ�CDE�����ֵ��
���������߶�BC�ϲ�����������D�㣬
��D��C���Ҳ�ʱ��S��CDE=
•
��a+4��a=
��
��ã�a=2����ʱD��
��
����
��D��B�����ʱ��S��CDE=
•
��a-4��a=
��
��ã�a=6����ʱD��-
��-
����
| 8 |
| 3 |
��ֱ����y��Ľ���P��0��
| 8 |
| 3 |
�ߡ�ACB=��POA=90�㣬��BAC=��PAO��
���ABC����APO��
��
| BC |
| OP |
| AB |
| AP |
��ֱ��l��y=-
| 4 |
| 3 |
| 8 |
| 3 |
��A��2��0����
��OP=
| 8 |
| 3 |
��AP=
| OA2+OP2 |
| 10 |
| 3 |
��
| BC | ||
|
| 5 | ||
|
��BC=4��

��2���������ۣ�
����D�ڵ�C��ߣ�
��CD=1��BC=4��
��BD1=3��
��BC��l��ֱ��l��y=-
| 4 |
| 3 |
| 8 |
| 3 |
��ֱ��BC��б��Ϊ
| 3 |
| 4 |
��
| OC |
| OB |
| 3 |
| 4 |
��sin��OBC=
| 3 |
| 5 |
| 4 |
| 5 |
��cos��OBC=
| BE1 |
| BD1 |
| 4 |
| 5 |
| D 1E1 |
| BD1 |
| 3 |
| 5 |
��BE1=
| 12 |
| 5 |
| 9 |
| 5 |
��OE1=OB-BE1=
| 3 |
| 5 |
��D1(-
| 3 |
| 5 |
| 9 |
| 5 |
����D�ڵ�C�ұߣ���BD2=5��ͬ����֤sin��OBC=
| D 2E2 |
| BD2 |
| 3 |
| 5 |
| BE2 |
| BD2 |
| 4 |
| 5 |
����D2 E2=3��BE2=4��
��OE2=4-3=1��
��D2 ��1��3����

����ͼ2��ʾ����CD=a����BD=4-a��
��m��l��BC��l
��BC��m
���BDE��ֱ�������Σ�
��tan��DBE=
| 3 |
| 4 |
��DE=
| 3 |
| 4 |
| 3 |
| 4 |
��S��CDE=
| 1 |
| 2 |
| 3 |
| 4 |
| 3 |
| 8 |
| 3 |
| 2 |
�൱a=2ʱ��CDE��������
��ʱD��-
| 7 |
| 5 |
| 6 |
| 5 |

����ͼ3��ʾ
��D���߶�BC��ʱ�����ڡ�CDE�����ֵ��
| 3 |
| 2 |
��D��C���Ҳ�ʱ��S��CDE=
| 1 |
| 2 |
| 3 |
| 4 |
| 9 |
| 2 |
��ã�a=2����ʱD��
| 9 |
| 5 |
| 18 |
| 5 |
��D��B�����ʱ��S��CDE=
| 1 |
| 2 |
| 3 |
| 4 |
| 9 |
| 2 |
��ã�a=6����ʱD��-
| 23 |
| 5 |
| 6 |
| 5 |
������������һ�κ������ۺ��⣬��Ҫ������ֱ����������Ľ����Լ�����ֱ�ߴ�ֱ��ƽ�е����ʣ����������Ƶ��ж������ʣ�ֱ�����Ǻ�����Ӧ�õȣ�����Ĺؼ��Ǹ������⿼��ȫ�棬�ֶ�������������ۣ�

��ϰ��ϵ�д�
 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�
�����Ŀ
 ��ͼ��С����ĩ������ŷ��ݣ����ݷɵ�C��ʱ���߳�Ϊ40�ף���ʱС������վ��A��������á�CBD=60�㣬ǣ����B�����1.5�ף����ʱ���������ĸ߶ȣ�����������ţ���
��ͼ��С����ĩ������ŷ��ݣ����ݷɵ�C��ʱ���߳�Ϊ40�ף���ʱС������վ��A��������á�CBD=60�㣬ǣ����B�����1.5�ף����ʱ���������ĸ߶ȣ�����������ţ���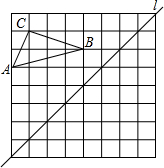 ��ͼ����8��8�������������У���֪��ABC�����������ڸ���ϣ�
��ͼ����8��8�������������У���֪��ABC�����������ڸ���ϣ� Ϊ���˽�ij����ѧ���������������ȡ��������ѧ���ڵ�λʱ���ڽ����������ϲ��ԣ����������ݣ����е�����Ϊ��������������Ƶ���ֲ�ֱ��ͼ����ͼ����
Ϊ���˽�ij����ѧ���������������ȡ��������ѧ���ڵ�λʱ���ڽ����������ϲ��ԣ����������ݣ����е�����Ϊ��������������Ƶ���ֲ�ֱ��ͼ����ͼ����