题目内容
在平行四边形ABCD中,∠B=120°,AE平分∠BAD交CD于点E,则∠AEC= .
考点:平行四边形的性质
专题:
分析:利用平行四边形的对角相等邻角互补进而得出∠D=120°,∠DAB=60°,再利用角平分线的性质和三角形外角的性质求出∠AEC的度数.
解答: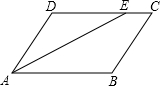 解:∵平行四边形ABCD中,∠B=120°,
解:∵平行四边形ABCD中,∠B=120°,
∴∠D=120°,∠DAB=60°,
∵AE平分∠BAD交CD于点E,
∴∠DAE=30°
则∠AEC=∠DAE=120°+30°=150°.
故答案为:150°.
 解:∵平行四边形ABCD中,∠B=120°,
解:∵平行四边形ABCD中,∠B=120°,∴∠D=120°,∠DAB=60°,
∵AE平分∠BAD交CD于点E,
∴∠DAE=30°
则∠AEC=∠DAE=120°+30°=150°.
故答案为:150°.
点评:此题主要考查了平行四边形的性质以及角平分线的性质和三角形外角的性质,得出∠D与∠DAE的度数是解题关键.

练习册系列答案
相关题目
下列式中计算的结果不是1的是( )
| A、-1+2 | ||||
| B、(3.14-π)0 | ||||
| C、(-1)2009 | ||||
D、(2+
|
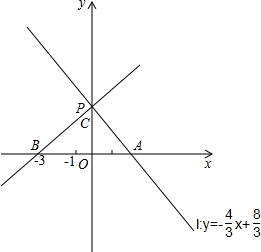 在平面直角坐标系中,点O是原点.直线l:y=
在平面直角坐标系中,点O是原点.直线l:y= 某种表面较粗糙的圆柱形罐头,如图,现有一只小蚂蚁欲从下底A处出发,爬行到上底的C处,则小蚂蚁爬行的最短路线长为
某种表面较粗糙的圆柱形罐头,如图,现有一只小蚂蚁欲从下底A处出发,爬行到上底的C处,则小蚂蚁爬行的最短路线长为