题目内容
10．已知关于x的方程x2-6x+k=0的两根分别是x1，x2，且$\frac{1}{{x}_{1}}$$+\frac{1}{{x}_{2}}$=3，则k的值是（ ）| A． | 1 | B． | 2 | C． | 3 | D． | 4 |
分析 由根与系数的关系可得x1+x2=6、x1•x2=k，将其代入$\frac{1}{{x}_{1}}$$+\frac{1}{{x}_{2}}$=$\frac{{x}_{1}+{x}_{2}}{{x}_{1}•{x}_{2}}$中可得出关于k的分式方程，解之并检验后即可得出结论．
解答 解：∵关于x的方程x2-6x+k=0的两根分别是x1，x2，
∴x1+x2=6，x1•x2=k，
∴$\frac{1}{{x}_{1}}$$+\frac{1}{{x}_{2}}$=$\frac{{x}_{1}+{x}_{2}}{{x}_{1}•{x}_{2}}$=$\frac{6}{k}$=3，
解得：k=2，
经检验，k=2是原方程的解，且符合题意．
故选B．
点评 本题考查了根与系数的关系，牢记“两根之和等于-$\frac{b}{a}$，两根之积等于$\frac{c}{a}$”是解题的关键．
练习册系列答案
考前必练系列答案
相关题目
20．下列式子计算正确的是（ ）
| A． | （-1）-1=1 | B． | （π-3.14）0=0 | C． | 24÷26=22 | D． | ${（{-\frac{1}{2}}）^{-3}}$=-8 |
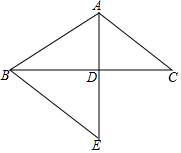如图，△ABC中，AB=AC，线段BC的垂直平分线AD交BC于点D，过点BE作BE∥AC，交AD的延长线于点E，求证：AB=BE．