��Ŀ����
�Ƿ��������k��ʹ������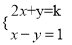 �Ľ��У�x����1��y������1�������ڣ����k��ֵ���������ڣ�˵�����ɣ�
�Ľ��У�x����1��y������1�������ڣ����k��ֵ���������ڣ�˵�����ɣ�
 kֻ��ȡ3��4��5
������������������������ʱ���Խ����Ԫһ�η�������x��y����k��ʽ�ӣ�Ȼ����k�ķ�Χ������֪��k��ȡֵ��
������������ⷽ�����
��x����1��y������1�Ӷ��ò���ʽ��
��֮��2��k��5
�֡�kΪ����
��kֻ��ȡ3��4��5
�𣺵�kΪ3��4��5ʱ��������Ľ��У�x����1��y������1��
kֻ��ȡ3��4��5
������������������������ʱ���Խ����Ԫһ�η�������x��y����k��ʽ�ӣ�Ȼ����k�ķ�Χ������֪��k��ȡֵ��
������������ⷽ�����
��x����1��y������1�Ӷ��ò���ʽ��
��֮��2��k��5
�֡�kΪ����
��kֻ��ȡ3��4��5
�𣺵�kΪ3��4��5ʱ��������Ľ��У�x����1��y������1��
 �п�������㾫��ϵ�д�
�п�������㾫��ϵ�д�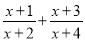 �ĺ���________
���________
 �����������������
��
��
����
�ʴ�Ϊ�� ��
�����������������
��
��
����
�ʴ�Ϊ�� �� ���в���ʽ�У���һԪһ�β���ʽ����( )
A. 2x-1��0 B. -1��2 C. 3x-2y��-1 D. y2+3��5
 A
��������A����һԪһ�β���ʽ��
B������δ֪���������϶��壻
C����������δ֪���������϶��壻
D��δ֪���Ĵ�����2�������϶��壻
��ѡA��
A
��������A����һԪһ�β���ʽ��
B������δ֪���������϶��壻
C����������δ֪���������϶��壻
D��δ֪���Ĵ�����2�������϶��壻
��ѡA�� ij�̳��Ƴ�һ�ֹ������ƾ���ڸ��̳�����ɰ���Ʒ�۸�İ����Żݣ���������ʱÿ��Ҫ��100Ԫ�����ѣ��谴����ۼƹ�����Ϊx��Ԫ������x��__ʱ����������ʡǮ��
 500
����������������
������ã�x��0.8x��100����ã�x��500��
�������������500Ԫʱ����������ʡǮ��
�ʴ�Ϊ��500��
500
����������������
������ã�x��0.8x��100����ã�x��500��
�������������500Ԫʱ����������ʡǮ��
�ʴ�Ϊ��500�� С������1.5�ף�С���ְ�����1.8�ף�С������һ��ÿ����a�ף���10����ƽ̨˵�����ְ֣���������������߶��Ȳ������ˣ����ɴ˿ɵù���a�IJ���ʽ�ǣ�������
A. 10a��1.8��2 B. 1.5+a+10��1.8��2 C. 10a+1.5��1.8��2 D. 1.8��2��10a+15
 C
������������С��������+10����̨�ĸ߶ȣ��ְ����ߵ�2����ʽ���ɣ�
��������
�������⣬��10a+1.5��1.8��2��
��ѡ��C��
C
������������С��������+10����̨�ĸ߶ȣ��ְ����ߵ�2����ʽ���ɣ�
��������
�������⣬��10a+1.5��1.8��2��
��ѡ��C�� ����ʽx��8��3x��5�������������_________��
 ��2
������������ʽx��8��3x��5�Ľ⼯Ϊx������
����������������ǩ�2��
��2
������������ʽx��8��3x��5�Ľ⼯Ϊx������
����������������ǩ�2�� ����ʽ��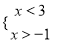 �Ľ⼯��_________��
�Ľ⼯��_________��
 ��1��x��3
�����������ݡ�С���С�м��ҡ���ԭ���������ʽ��Ľ⼯���ɣ�
�ߩ�1��3��
��˲���ʽ��Ľ⼯Ϊ����1��x��3��
�ʴ�Ϊ����1��x��3��
��1��x��3
�����������ݡ�С���С�м��ҡ���ԭ���������ʽ��Ľ⼯���ɣ�
�ߩ�1��3��
��˲���ʽ��Ľ⼯Ϊ����1��x��3��
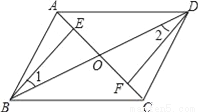
�ʴ�Ϊ����1��x��3�� ��ͼ���ı���ABCD�У��Խ���AC��BD�ཻ�ڵ�O����E��F�ֱ���OA��OC��
��1������������������OB=OD���ڡ�1=��2����OE=OF���������ѡȡ��������֤����BEO�ա�DFO��
��2���ڣ�1������������ѡ������ǰ���£�����AE=CF����֤���ı���ABCD��ƽ���ı��Σ�
 ��1������������2��������.
�������������������1��ѡȡ�٢ڣ�����ASA�ж���BEO�ա�DFO��Ҳ��ѡȡ�ڢۣ�����AAS�ж���BEO�ա�DFO������ѡȡ�٢ۣ�����SAS�ж���BEO�ա�DFO��
��2�����ݡ�BEO�ա�DFO�ɵ�EO��FO��BO��DO���ٸ��ݵ�ʽ�����ʿɵ�AO��CO�����������Խ�����ƽ�ֵ��ı�����ƽ���ı��οɵý��ۣ�
���������
֤������1��ѡȡ�٢ڣ�
...
��1������������2��������.
�������������������1��ѡȡ�٢ڣ�����ASA�ж���BEO�ա�DFO��Ҳ��ѡȡ�ڢۣ�����AAS�ж���BEO�ա�DFO������ѡȡ�٢ۣ�����SAS�ж���BEO�ա�DFO��
��2�����ݡ�BEO�ա�DFO�ɵ�EO��FO��BO��DO���ٸ��ݵ�ʽ�����ʿɵ�AO��CO�����������Խ�����ƽ�ֵ��ı�����ƽ���ı��οɵý��ۣ�
���������
֤������1��ѡȡ�٢ڣ�
... ��ͼ����?ABCD�У�AB=12��AD=8����ABC��ƽ���߽�CD�ڵ�F����AD���ӳ����ڵ�E��CG��BE������ΪG����EF=2�����߶�CG�ij�Ϊ��������
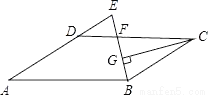
A. 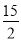 B.
B. 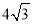 C.
C. 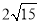 D.
D. 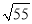
 C
���������ߡ�ABC��ƽ���߽�CD�ڵ�F��
���ABE=��CBE��
���ı���ABCD��ƽ���ı��Σ�
��DC��AB��
���CBE=��CFB=��ABE=��E��
��CF=BC=AD=8��AE=AB=12��
��AD=8��
��DE=4��
��DC��AB��
�࣬
�࣬
��EB=6��
��CF=CB��CG��BF��
��BG=BF=2...
C
���������ߡ�ABC��ƽ���߽�CD�ڵ�F��
���ABE=��CBE��
���ı���ABCD��ƽ���ı��Σ�
��DC��AB��
���CBE=��CFB=��ABE=��E��
��CF=BC=AD=8��AE=AB=12��
��AD=8��
��DE=4��
��DC��AB��
�࣬
�࣬
��EB=6��
��CF=CB��CG��BF��
��BG=BF=2... 
