题目内容
6.圆中与半径相等的弦所对的圆周角度数是( )| A. | 30° | B. | 60° | C. | 150° | D. | 30°或 150° |
分析 根据题意画出几何图,易得△OAB为等边三角形,则∠AOB=60°,于是根据圆周角定理得到∠ACB=$\frac{1}{2}$∠AOB=30°,然后根据圆内接四边形的性质求出∠ADB的度数,这样得到弦AB所对的圆周角的度数.
解答  解:如图,∵AB=OB=OA,
解:如图,∵AB=OB=OA,
∴△OAB为等边三角形,
∴∠AOB=60°,
∴∠ACB=$\frac{1}{2}$∠AOB=30°,
∴∠ADB=180°-∠ACB=150°,
∴弦AB所对的圆周角的度数为30°或150°.
故选D.
点评 本题考查的是圆周角定理,熟知在同圆或等圆中,同弧或等弧所对的圆周角相等,都等于这条弧所对的圆心角的一半角是解答此题的关键.

练习册系列答案
相关题目
17. 如图,下面是一个简单的数值运算程序,当输入x的值为2时,输出的数值是( )
如图,下面是一个简单的数值运算程序,当输入x的值为2时,输出的数值是( )
 如图,下面是一个简单的数值运算程序,当输入x的值为2时,输出的数值是( )
如图,下面是一个简单的数值运算程序,当输入x的值为2时,输出的数值是( )| A. | 0 | B. | -9 | C. | 6 | D. | -6 |
15.下列语句中正确的是( )
| A. | 边数越多的多边形,它的内角和也越大 | |
| B. | 多边形随着边数的增加,它的外角和和随着增加 | |
| C. | 当多边形的边数扩大两倍时,多边形的内角和也扩大两倍 | |
| D. | 当边数超过4时,多边形的内角一定大于相邻的外角 |
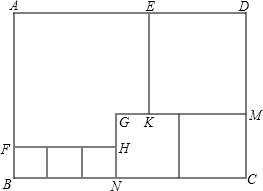 如图所示,用三种大小不等的正方形和一个缺角的正方形拼成一个长方形ABCD(不重叠且没有缝隙),若GH=GK=1,设BF=x.
如图所示,用三种大小不等的正方形和一个缺角的正方形拼成一个长方形ABCD(不重叠且没有缝隙),若GH=GK=1,设BF=x. 如图,正方形ABCD,曲线DP1P2P3P4P5…叫做“正方形的渐开线”,其中弧DP1,弧P1P2,弧P2P3,弧P3P4,弧P4P5…的圆心依次按点A,B,C,D,A循环,它们的弧长分别记为l1,l2,l3,l4,l5….当AB=1时,l2011等于$\frac{2011π}{2}$.
如图,正方形ABCD,曲线DP1P2P3P4P5…叫做“正方形的渐开线”,其中弧DP1,弧P1P2,弧P2P3,弧P3P4,弧P4P5…的圆心依次按点A,B,C,D,A循环,它们的弧长分别记为l1,l2,l3,l4,l5….当AB=1时,l2011等于$\frac{2011π}{2}$.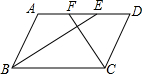 如图,平行四边形ABCD中,AB=2cm,BC=3cm,∠ABC,∠BCD的平分线分别交AD于点F、E,则EF的长为1cm.
如图,平行四边形ABCD中,AB=2cm,BC=3cm,∠ABC,∠BCD的平分线分别交AD于点F、E,则EF的长为1cm.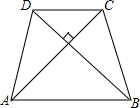 如图,等腰梯形ABCD的面积为100cm2,AC⊥BD.
如图,等腰梯形ABCD的面积为100cm2,AC⊥BD.