题目内容
17．
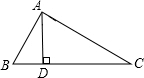如图，在△ABC中，AD⊥BC于点D，若AD=4，BD=2，CD=8，那么△ABC是直角三角形吗？为什么？
分析 在Rt△ABD中利用勾股定理可求AB2，同理在Rt△ACD中利用勾股定理可求AC2，而BC=CD+BD=10，易求AC2+AB2=100=BC2，从而可知△ABC是直角三角形．
解答 解：△ABC是直角三角形，理由如下：
∵AD⊥BC，AD=4，BD=2，
∴AB2=AD2+BD2=20，
又∵AD⊥BC，CD=8，AD=4，
∴AC2=CD2+AD2=80，
∵BC=CD+BD=10，
∴BC2=100，
∴AC2+AB2=100=BC2，
∴△ABC是直角三角形．
点评 本题考查勾股定理、勾股定理的逆定理的应用．判断三角形是否为直角三角形，已知三角形三边的长，只要利用勾股定理的逆定理加以判断即可．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
9．
如图，在△ABC中，∠A=110°，DE∥CB，若∠CDE=140°，则∠B的度数为（ ）
如图，在△ABC中，∠A=110°，DE∥CB，若∠CDE=140°，则∠B的度数为（ ）| A． | 20° | B． | 30° | C． | 35° | D． | 40° |
6．若x满足x2=$\frac{9}{4}$，则x的值为（ ）
| A． | $\frac{3}{2}$ | B． | -$\frac{3}{2}$ | C． | ±$\frac{3}{2}$ | D． | ±$\frac{2}{3}$ |
8．
如图所示，有理数a、b在数轴上的位置如图，则下列说法错误的是（ ）
如图所示，有理数a、b在数轴上的位置如图，则下列说法错误的是（ ）| A． | b＜a | B． | a+b＜0 | C． | ab＜0 | D． | b-a＞0 |
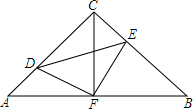如图，在△ABC中，∠A=∠B=45°，AC=8，F是AB边上的中点，点D，E分别在AC，BC上，且AD=CE，CF=AF．则四边形CDFE的面积是16．