题目内容
13.已知y=$\sqrt{9-x}$+$\sqrt{x-9}$-1,求yx的值.分析 首先根据二次根式中的被开方数是非负数,可得$\left\{\begin{array}{l}{9-x≥0}\\{x-9≤0}\end{array}\right.$;据此求出x的值是9;然后把求出的x的值代入算式y=$\sqrt{9-x}$+$\sqrt{x-9}$-1,求出y的值是多少,进而求出yx的值是多少即可.
解答 解:∵二次根式中的被开方数是非负数,
∴$\left\{\begin{array}{l}{9-x≥0}\\{x-9≤0}\end{array}\right.$
解得x=9,
∴y=$\sqrt{9-x}$+$\sqrt{x-9}$-1=0+0-1=-1,
∴yx=(-1)9=-1,
即yx的值是-1.
点评 此题主要考查了二次根式有意义的条件,要熟练掌握,解答此题的关键是要明确:二次根式中的被开方数是非负数,并能求出x、y的值各是多少.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
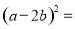 ____________________。
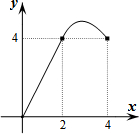
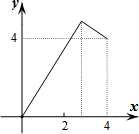
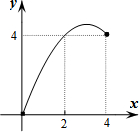
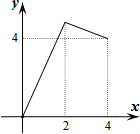
____________________。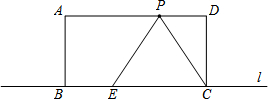 矩形ABCD的边BC在直线l上,AB=2,BC=4,P是AD边上一动点且不与点D重合,连结CP,过点P作∠APE=∠CPD,交直线l于点E,若PD的长为x,△PEC与矩形ABCD重合部分的面积为y,则下列图象中,能表示y与x的函数关系的图象大致是( )
矩形ABCD的边BC在直线l上,AB=2,BC=4,P是AD边上一动点且不与点D重合,连结CP,过点P作∠APE=∠CPD,交直线l于点E,若PD的长为x,△PEC与矩形ABCD重合部分的面积为y,则下列图象中,能表示y与x的函数关系的图象大致是( )