题目内容
15.已知$\sqrt{a-1}$+$\sqrt{1-a}$有意义,且|b-3|+$\sqrt{c-2}$+(d-2015)2=0,求($\sqrt{2}$)-a+($\sqrt{2}$)b+($\frac{1}{\sqrt{2}-1}$)c+(-1)d=( )| A. | 4$\sqrt{2}$+2 | B. | 3 | C. | $\frac{9}{2}$$\sqrt{2}$+2 | D. | 3+2$\sqrt{2}$ |
分析 首先由非负数的性质和二次根式的意义得出a=1,b=3,c=2,d=2015,进一步代入求得答案即可.
解答 解:∵$\sqrt{a-1}$+$\sqrt{1-a}$,|b-3|+$\sqrt{c-2}$+(d-2015)2=0,
∴a=1,b=3,c=2,d=2015,
∴($\sqrt{2}$)-a+($\sqrt{2}$)b+($\frac{1}{\sqrt{2}-1}$)c+(-1)d
=$\frac{\sqrt{2}}{2}$+2$\sqrt{2}$+($\sqrt{2}$+1)2-1
=$\frac{9}{2}$$\sqrt{2}$+2.
故选:C.
点评 此题考查了二次根式的化简求值,涉及的知识有:二次根式的意义,非负数的性质,代数式的求值,熟练掌握非负数的性质是解本题的关键.

练习册系列答案
 53随堂测系列答案
53随堂测系列答案
相关题目
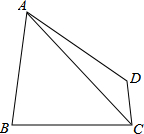 如图,在四边形ABCD中,AD=AB=BC,连接AC,且∠ACD=30°,tan∠BAC=$\frac{{2\sqrt{3}}}{3}$,CD=3,则AC=6$\sqrt{3}$.
如图,在四边形ABCD中,AD=AB=BC,连接AC,且∠ACD=30°,tan∠BAC=$\frac{{2\sqrt{3}}}{3}$,CD=3,则AC=6$\sqrt{3}$.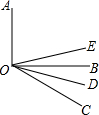 如图所示,已知OE是∠AOC的平分线,OD是∠BOC的平分线.若∠AOC=120°,∠BOC=β,求∠DOE.
如图所示,已知OE是∠AOC的平分线,OD是∠BOC的平分线.若∠AOC=120°,∠BOC=β,求∠DOE.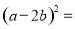 ____________________。
____________________。