题目内容
17.定义 $|\begin{array}{l}{a}&{b}\\{c}&{d}\end{array}|$为二阶行列式.规定它的运算法则为$|\begin{array}{l}{a}&{b}\\{c}&{d}\end{array}|$=ad-bc.那么当x=1时,二阶行列式$|\begin{array}{l}{x+1}&{1}\\{0}&{x-1}\end{array}|$的值为0.分析 根据题目中的新运算,可以求得题目中的二阶行列式的值.
解答 解:∵$|\begin{array}{l}{a}&{b}\\{c}&{d}\end{array}|$=ad-bc,
∴$|\begin{array}{l}{x+1}&{1}\\{0}&{x-1}\end{array}|$
=(x+1)(x-1)-1×0
=x2-1-0
=x2-1,
当x=1时,原式=12-1=0,
故答案为:0.
点评 本题考查整式的混合运算、新运算,解题的关键是明确行列式的计算方法.

练习册系列答案
相关题目
5.关于$\sqrt{5}$的叙述,正确的是( )
| A. | $\sqrt{5}$是有理数 | B. | 5的平方根是$\sqrt{5}$ | ||
| C. | 2<$\sqrt{5}$<3 | D. | 在数轴上不能找到表示$\sqrt{5}$的点 |

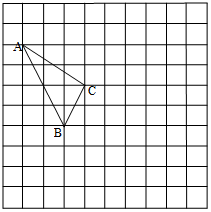 在如图所示的正方形网格中,每个小正方形的边长为1,格点三角形(顶点是网格线的交点的三角形)ABC的顶点A、C的坐标分别为(-4,3)、(-1,1).
在如图所示的正方形网格中,每个小正方形的边长为1,格点三角形(顶点是网格线的交点的三角形)ABC的顶点A、C的坐标分别为(-4,3)、(-1,1).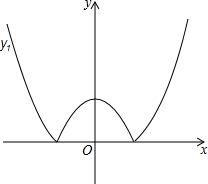 如图,将二次函数y=x2-m(其中m>0)的图象在x轴下方的部分沿x轴翻折,图象的其余部分保持不变,形成新的图象记为y1,另有一次函数y=x+b的图象记为y2,则以下说法:
如图,将二次函数y=x2-m(其中m>0)的图象在x轴下方的部分沿x轴翻折,图象的其余部分保持不变,形成新的图象记为y1,另有一次函数y=x+b的图象记为y2,则以下说法: