题目内容
9.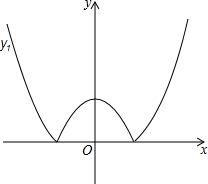 如图,将二次函数y=x2-m(其中m>0)的图象在x轴下方的部分沿x轴翻折,图象的其余部分保持不变,形成新的图象记为y1,另有一次函数y=x+b的图象记为y2,则以下说法:
如图,将二次函数y=x2-m(其中m>0)的图象在x轴下方的部分沿x轴翻折,图象的其余部分保持不变,形成新的图象记为y1,另有一次函数y=x+b的图象记为y2,则以下说法:①当m=1,且y1与y2恰好有三个交点时b有唯一值为1;
②当b=2,且y1与y2恰有两个交点时,m>4或0<m<$\frac{7}{4}$;
③当m=-b时,y1与y2一定有交点;
④当m=b时,y1与y2至少有2个交点,且其中一个为(0,m).
其中正确说法的序号为②④.
分析 ①错误.如图1中,当直线y=x+b与抛物线相切时,也满足条件只有三个交点.此时b≠1,故①错误.
②正确.如图2中,当抛物线经过点(-2,0)时,0=4-m,m=4,观察图象可知m>4时,y1与y2恰有两个交点.
③错误.如图3中,当b=-4时,观察图象可知,y1与y2没有交点,故③错误.
④正确.如图4中,当b=4时,观察图象可知,b>0,y1与y2至少有2个交点,且其中一个为(0,b),故④正确.
解答 解:①错误.如图1中,当直线y=x+b与抛物线相切时,也满足条件只有三个交点.此时b≠1,故①错误.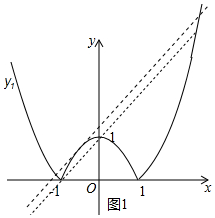
②正确.如图2中,当抛物线经过点(-2,0)时,0=4-m,m=4,观察图象可知m>4时,y1与y2恰有两个交点.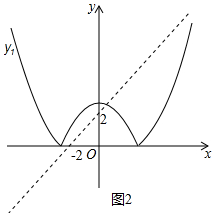
由$\left\{\begin{array}{l}{y=x+2}\\{y=-{x}^{2}+m}\end{array}\right.$消去y得到x2+x+2-m=0,当△=0时,1-8+4m=0,
∴m=$\frac{7}{4}$,
观察图象可知当0<m<$\frac{7}{4}$时,y1与y2恰有两个交点.故②正确.
③错误.如图3中,当b=-4时,观察图象可知,y1与y2没有交点,故③错误.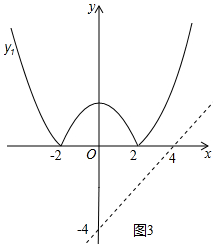
④正确.如图4中,当b=4时,观察图象可知,b>0,y1与y2至少有2个交点,且其中一个为(0,b),故④正确.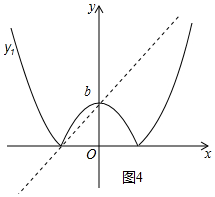
故答案为②④
点评 本题考查二次函数与x轴的交点、一次函数的应用、函数与方程的关系等知识,解题的关键是学会利用函数图象解决问题,学会利用根的判别式解决函数图象的交点问题,属于中考常考题型.

练习册系列答案
相关题目
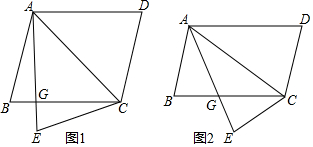
 如图所示,已知点E是四边形ABCD内的一点,若AE平分∠BAD,BE平分∠ABC,且∠1+∠2=90°,试说明AD与BC的位置关系.
如图所示,已知点E是四边形ABCD内的一点,若AE平分∠BAD,BE平分∠ABC,且∠1+∠2=90°,试说明AD与BC的位置关系.