题目内容
4.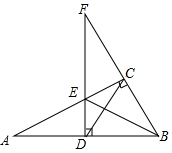 在Rt△ABC中,∠ACB=90°,AB的垂直平分线DE交BC的延长线于点F,连接CD、BE,若EF=AE.
在Rt△ABC中,∠ACB=90°,AB的垂直平分线DE交BC的延长线于点F,连接CD、BE,若EF=AE.(1)求证:△ADE≌△FCE;
(2)问∠ABE=∠EBF吗?说说你的理由
(3)写出图中所有的等腰三角形.
分析 (1)由条件可求得∠A=∠F,可证得△ADE≌△FCE;
(2)由(1)可得DE=CE,由角平分线的判定可知BE平分∠ABC,可求得∠ABE=∠EBF;
(3)结合(1)、(2)可写出等腰三角形.
解答 (1)证明:
∵DE垂直平分AB,
∴∠ADE=∠ACB=∠ECF=90°,
∴∠A+∠ABC=∠F+∠ABC,
∴∠A=∠F,
在△ADE和△FCE中
$\left\{\begin{array}{l}{∠A=∠F}\\{∠ADE=∠FCE}\\{AE=EF}\end{array}\right.$
∴△ADE≌△FCE(AAS);
(2)解:相等,
理由如下:
∵△ADE≌△FCE,
∴DE=CE,
∵ED⊥AB,EC⊥BF,
∴点D在∠ABF的平分线上,
∴∠ABE=∠EBF;
(3)解:
由(1)可知△ADE≌△FCE,
∴CE=DE,
由(2)可知BE平分∠ABF,
∴∠DBE=∠CBE,
在△DBE和△CBE中
$\left\{\begin{array}{l}{∠EDB=∠ECB}\\{∠EBD=∠EBC}\\{DE=CE}\end{array}\right.$
∴△DBE≌△CBE(AAS),
∴BC=BD,
∴等腰三角形有△ABE、△FEB、△BCD和△ECD.
点评 本题主要考查全等三角形的判定和性质,掌握全等三角形的判定方法(即SSS、SAS、ASA、AAS和HL)和全等三角形的性质(即对应边相等、对应角相等).

练习册系列答案
 心算口算巧算一课一练系列答案
心算口算巧算一课一练系列答案
相关题目
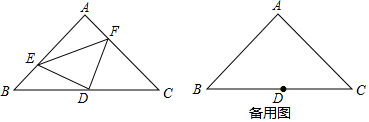
 如图,△ABC中,AB=AC,PB=PC,连接AP并延长交BC于D,求证:AD垂直平分BC.
如图,△ABC中,AB=AC,PB=PC,连接AP并延长交BC于D,求证:AD垂直平分BC.
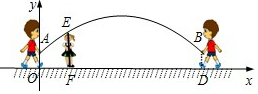 跳绳时,绳甩到最高处时的形状是抛物线.正在甩绳的甲、乙两名同学拿绳的手间距AB为6米,到地面的距离AO和BD均为0.9米,身高为1.4米的小丽站在距点O的水平距离为1米的点F处,绳子甩到最高处时刚好通过她的头顶点E.以点O为原点建立如图所示的平面直角坐标系,设此抛物线的解析式为y=ax2+bx+0.9.
跳绳时,绳甩到最高处时的形状是抛物线.正在甩绳的甲、乙两名同学拿绳的手间距AB为6米,到地面的距离AO和BD均为0.9米,身高为1.4米的小丽站在距点O的水平距离为1米的点F处,绳子甩到最高处时刚好通过她的头顶点E.以点O为原点建立如图所示的平面直角坐标系,设此抛物线的解析式为y=ax2+bx+0.9.