题目内容
14.如图1,在半径为5的⊙O中,AB是直径,点C在⊙O上,CD是⊙O的切线,AD⊥CD于D.(1)求证:AC平分∠DAB;
(2)如图2,AD交⊙O于F,AF=6,E是半圆的中点,连接FE交AC于G,求S△AFG.
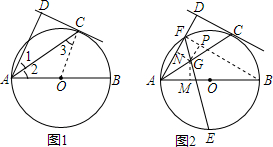
分析 (1)由CD与⊙O相切,AD⊥CD,可得AD∥OC,继而可得∠CAD=∠CAO,即AC平分∠DAB;
(2)连接BF,分别作GM⊥AB于M,GN⊥AF于N,GP⊥FB于P,根据圆周角定理得到∠AFB=90°,AB=10,根据勾股定理得到BF=$\sqrt{1{0}^{2}-{6}^{2}}$=8,由已知条件得到∠3=∠4,推出点G为⊙O的内心,M、N、P是△FAB内切圆与三边的切点,于是得到GM=GN=GP,AM=AN,BM=BP,FN=FP.求得FN=(6+8-10)÷2=2.GN=FN=2.即可得到结论.
解答  解:(1)连接OC,
解:(1)连接OC,
∵CD与⊙O相切,
∴OC⊥CD,
又∵AD⊥CD,
∴AD∥OC,
∴∠1=∠3,
∵OA=OC,
∴∠2=∠3,
∴∠1=∠2,
∴AC平分∠DAB;
(2)连接BF,分别作GM⊥AB于M,GN⊥AF于N,GP⊥FB于P,
∵AB是直径,半径为5,
∴∠AFB=90°,AB=10,
又∵AF=6,
∴BF=$\sqrt{1{0}^{2}-{6}^{2}}$=8,
∵点E是半圆的中点,
∴∠3=∠4,
又∵∠1=∠2,
∴点G为⊙O的内心,M、N、P是△FAB内切圆与三边的切点,
∴GM=GN=GP,AM=AN,BM=BP,FN=FP.
∴FN=(6+8-10)÷2=2.GN=FN=2.
∴S△AFG=0.5AF•GN=0.5×6×2=6.
点评 此题考查了切线的性质、正方形的判定与性质、切线长定理以及内切圆的性质.此题难度适中,注意掌握数形结合思想与方程思想的应用.

练习册系列答案
相关题目
4.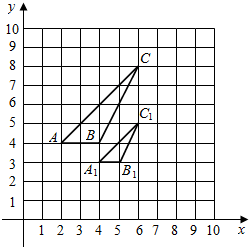 如图,△ABC与△A1B1C1是位似图形,且顶点都在格点上,则位似中心坐标是( )
如图,△ABC与△A1B1C1是位似图形,且顶点都在格点上,则位似中心坐标是( )
 如图,△ABC与△A1B1C1是位似图形,且顶点都在格点上,则位似中心坐标是( )
如图,△ABC与△A1B1C1是位似图形,且顶点都在格点上,则位似中心坐标是( )| A. | (6,2) | B. | (6,1) | C. | (4,2) | D. | (2,6) |
 △ABC中,∠C=90°,∠ABC=45°,D为AC上一点,∠DBC=30°,求AD:AB的值.
△ABC中,∠C=90°,∠ABC=45°,D为AC上一点,∠DBC=30°,求AD:AB的值.