题目内容
5.计算:(-3)0-|2-$\sqrt{12}$|-(-1)-2+4sin60°.分析 原式利用零指数幂、负整数指数幂法则,绝对值的代数意义,以及特殊角的三角函数值计算即可得到结果.
解答 解:原式=1-2$\sqrt{3}$+2-1+2$\sqrt{3}$=2.
点评 此题考查了实数的运算,零指数幂、负整数指数幂,熟练掌握运算法则是解本题的关键.

练习册系列答案
 名题训练系列答案
名题训练系列答案 期末集结号系列答案
期末集结号系列答案
相关题目
16.已知a=$\sqrt{2}$+1,b=$\frac{1}{\sqrt{2}-1}$,则a,b的大小关系是( )
| A. | a>b | B. | a=b | C. | a<b | D. | 无法确定 |
13. 如图,直线a∥b,直线c分别与a,b相交于A,C两点,AC⊥AB于点A,AB交直线b于点B,若∠1=40°,则∠ABC的度数为( )
如图,直线a∥b,直线c分别与a,b相交于A,C两点,AC⊥AB于点A,AB交直线b于点B,若∠1=40°,则∠ABC的度数为( )
 如图,直线a∥b,直线c分别与a,b相交于A,C两点,AC⊥AB于点A,AB交直线b于点B,若∠1=40°,则∠ABC的度数为( )
如图,直线a∥b,直线c分别与a,b相交于A,C两点,AC⊥AB于点A,AB交直线b于点B,若∠1=40°,则∠ABC的度数为( )| A. | 52° | B. | 50° | C. | 45° | D. | 40° |
20.抛物线y=(x+5)2-1先向右平移4个单位,再向上平移4个单位,得到抛物线的解析式为( )
| A. | y=x2+18x+84 | B. | y=x2+2x+4 | C. | y=x2+18x+76 | D. | y=x2+2x-2 |
10.当x( )时,分式$\frac{x+1}{1+\frac{4}{x+2}}$有意义.
| A. | 等于-2 | B. | 不等于-2 | C. | 等于-2或-6 | D. | ≠2和-6 |
17.-2的绝对值是( )
| A. | $\frac{1}{2}$ | B. | -2 | C. | 2 | D. | -$\frac{1}{2}$ |
14.一个不透明的口袋中有红色、黑色、白色的玻璃球共40个,这些球除颜色外都相同,小李将口袋中的球搅拌均匀,从中随机摸出一个球,记下它的颜色后再放回口袋中,不断重复这一过程,通过大量摸球试验后,统计结果显示摸到红色球、黑色球的频率稳定在15%和45%,则口袋中白色球的个数很可能是( )
| A. | 24 | B. | 20 | C. | 18 | D. | 16 |
15.一元一次不等式-2x+4≥0的解集在数轴上表示为( )
| A. |  | B. |  | C. |  | D. |  |
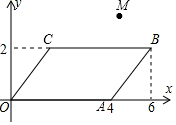 如图,在平面直角坐标系xOy中,四边形OABC是平行四边形,且A(4,0)、B(6,2)、M(4,3).在平面内有一条过点M的直线将平行四边形OABC的面积分成相等的两部分,请写出该直线的函数表达式y=2x-5.
如图,在平面直角坐标系xOy中,四边形OABC是平行四边形,且A(4,0)、B(6,2)、M(4,3).在平面内有一条过点M的直线将平行四边形OABC的面积分成相等的两部分,请写出该直线的函数表达式y=2x-5.