题目内容
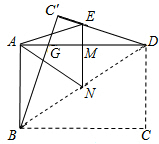 如图,一张矩形纸片ABCD,其中AD=8cm,AB=6cm,先沿对角线BD对折,点C落在点C′的位置,BC′交AD于点G.再折叠一次,使点D与点A重合,得折痕EN,EN交AD于点M,则EM的长为
如图,一张矩形纸片ABCD,其中AD=8cm,AB=6cm,先沿对角线BD对折,点C落在点C′的位置,BC′交AD于点G.再折叠一次,使点D与点A重合,得折痕EN,EN交AD于点M,则EM的长为考点:翻折变换(折叠问题)
专题:计算题
分析:根据矩形的性质得CD=AB=6,AD=BC=8,AD∥BC,由平行线的性质得∠ADB=∠CBD,再利用折叠的性质得到∠CBD=∠C′BD,BC′=BC=8,DC′=DC=6,
则∠GBD=∠GDB,所以GB=GD,设DG=x,则BG=x,AG=8-x,在Rt△ABG中,根据勾股定理得62+(8-x)2=x2,解得x=
,则GC′=BC′-BG=
,然后再根据折叠的性质得EN垂直平分AD,所以∠EMD=90°,DM=
AD=4,接着证明Rt△DEM∽Rt△DGC′,利用相似比计算EM的长.
则∠GBD=∠GDB,所以GB=GD,设DG=x,则BG=x,AG=8-x,在Rt△ABG中,根据勾股定理得62+(8-x)2=x2,解得x=
| 25 |
| 4 |
| 7 |
| 4 |
| 1 |
| 2 |
解答:解:∵四边形ABCD为矩形,
∴CD=AB=6,AD=BC=8,AD∥BC,
∴∠ADB=∠CBD,
∵矩形ABCD沿对角线BD对折,点C落在点C′的位置,BC′交AD于点G,
∴∠CBD=∠C′BD,BC′=BC=8,DC′=DC=6,
∴∠GBD=∠GDB,
∴GB=GD,
设DG=x,则BG=x,AG=8-x,
在Rt△ABG中,
∵AB2+AG2=BG2,
∴62+(8-x)2=x2,解得x=
,
∴GC′=BC′-BG=8-
=
,
∵折叠矩形ABCD一次,使点D与点A重合,得折痕EN,EN交AD于点M,
∴EN垂直平分AD,
∴∠EMD=90°,DM=
AD=4,
∵∠EDM=∠GDC′,
∴Rt△DEM∽Rt△DGC′,
∴
=
,即
=
,
∴EM=
.
故答案为
.
∴CD=AB=6,AD=BC=8,AD∥BC,
∴∠ADB=∠CBD,
∵矩形ABCD沿对角线BD对折,点C落在点C′的位置,BC′交AD于点G,
∴∠CBD=∠C′BD,BC′=BC=8,DC′=DC=6,
∴∠GBD=∠GDB,
∴GB=GD,
设DG=x,则BG=x,AG=8-x,
在Rt△ABG中,
∵AB2+AG2=BG2,
∴62+(8-x)2=x2,解得x=
| 25 |
| 4 |
∴GC′=BC′-BG=8-
| 25 |
| 4 |
| 7 |
| 4 |
∵折叠矩形ABCD一次,使点D与点A重合,得折痕EN,EN交AD于点M,
∴EN垂直平分AD,
∴∠EMD=90°,DM=
| 1 |
| 2 |
∵∠EDM=∠GDC′,
∴Rt△DEM∽Rt△DGC′,
∴
| EM |
| GC′ |
| DM |
| DC′ |
| EM | ||
|
| 4 |
| 6 |
∴EM=
| 7 |
| 6 |
故答案为
| 7 |
| 6 |
点评:本题考查了折叠的性质:折叠是一种对称变换,它属于轴对称,折叠前后图形的形状和大小不变,位置变化,对应边和对应角相等.也考查了矩形的性质勾股定理和相似三角形的判定与性质.

练习册系列答案
 永乾教育寒假作业快乐假期延边人民出版社系列答案
永乾教育寒假作业快乐假期延边人民出版社系列答案
相关题目
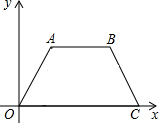 如图,在直角坐标平面内,四边形OABC是等腰梯形,其中OA=AB=BC=4,tan∠BCO=
如图,在直角坐标平面内,四边形OABC是等腰梯形,其中OA=AB=BC=4,tan∠BCO= 如图,正比例函数y1与反比例函数y2相交于点E(-1,2),若y1>y2>0,则x的取值范围是
如图,正比例函数y1与反比例函数y2相交于点E(-1,2),若y1>y2>0,则x的取值范围是 如图,AB是⊙O的直径,弦CD⊥AB,∠CDB=22.5°,CD=6,则扇形BOC的面积为
如图,AB是⊙O的直径,弦CD⊥AB,∠CDB=22.5°,CD=6,则扇形BOC的面积为 如图,在Rt△ABC中,AC=4,∠ACB=90°,∠B=30°.AD平分∠CAB交CB于D,点E是斜边AB上的一点,连接DE,当△ADE为直角三角形时,BE的长为
如图,在Rt△ABC中,AC=4,∠ACB=90°,∠B=30°.AD平分∠CAB交CB于D,点E是斜边AB上的一点,连接DE,当△ADE为直角三角形时,BE的长为 如图,在矩形纸片ABCD中,AB=4,AD=3,折叠纸片使DA与对角线DB重合,点A落在点A′处,折痕为DE,则A′E的长是
如图,在矩形纸片ABCD中,AB=4,AD=3,折叠纸片使DA与对角线DB重合,点A落在点A′处,折痕为DE,则A′E的长是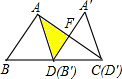 如图,在Rt△ABC中,AB=3,BC=5,∠BAC=90°,D是斜边BC的中点,将△ABD沿BC方向移动,使得点B与点D恰好重合,得到△A′B′D′,A′B′与AC相交于点F,则图中阴影部分(△ADF)的面积为
如图,在Rt△ABC中,AB=3,BC=5,∠BAC=90°,D是斜边BC的中点,将△ABD沿BC方向移动,使得点B与点D恰好重合,得到△A′B′D′,A′B′与AC相交于点F,则图中阴影部分(△ADF)的面积为