题目内容
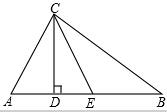 已知在△ABC中,∠ACB=90°,AB=2AC,CD和CE分别是AB边上的高线及中线,求∠ECD的度数.
已知在△ABC中,∠ACB=90°,AB=2AC,CD和CE分别是AB边上的高线及中线,求∠ECD的度数.考点:直角三角形斜边上的中线,等边三角形的判定与性质
专题:
分析:由已知条件易判定∠B=30°,则∠A=90°-30°=60°;根据直角三角形斜边上的中线等于斜边的一半和等腰三角形的性质可以求得∠A=∠AEC=60°;然在直角△ECD中,利用直角三角形的两个锐角互余的性质来求∠ECD的度数.
解答: 解:如图,∵在△ABC中,∠ACB=90°,AB=2AC,
解:如图,∵在△ABC中,∠ACB=90°,AB=2AC,
∴∠B=30°,
∴∠A=60°.
又∵CE是AB边上的中线,
∴EC=AE,
∴∠A=∠AEC=60°.
而CD是AB边上的高线,
∴∠CDE=90°,
∴∠ECD=90°-∠DEC=30°,即∠ECD=30°.
 解:如图,∵在△ABC中,∠ACB=90°,AB=2AC,
解:如图,∵在△ABC中,∠ACB=90°,AB=2AC,∴∠B=30°,
∴∠A=60°.
又∵CE是AB边上的中线,
∴EC=AE,
∴∠A=∠AEC=60°.
而CD是AB边上的高线,
∴∠CDE=90°,
∴∠ECD=90°-∠DEC=30°,即∠ECD=30°.
点评:本题考查了直角三角形斜边上的中线的性质:直角三角形斜边上的中线等于斜边的一半.

练习册系列答案
相关题目
有1角、5角、1元三种硬币15枚,共7元,则这三种硬币各有( )
| A、3枚、7枚、5枚 |
| B、5枚、7枚、3枚 |
| C、7枚、5枚、3枚 |
| D、3枚、5枚、7枚 |
 如图,AD∥EG∥BC,AD=6,BC=9,AE:AB=2:3,求GF的长.
如图,AD∥EG∥BC,AD=6,BC=9,AE:AB=2:3,求GF的长.
 AB是⊙O的直径,D是
AB是⊙O的直径,D是