题目内容
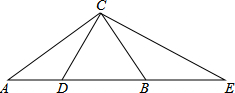 如图,在Rt△ABC中,∠ACB=90°,AC=b,AB=c,若D、E分别是AB和AB延长线上的两点,BD=BC,CE⊥CD,以AD和AE的长为根的一元二次方程是
如图,在Rt△ABC中,∠ACB=90°,AC=b,AB=c,若D、E分别是AB和AB延长线上的两点,BD=BC,CE⊥CD,以AD和AE的长为根的一元二次方程是考点:勾股定理,根与系数的关系,直角三角形斜边上的中线
专题:
分析:设BC=a,根据等边对等角可得∠BDC=∠BCD,再根据等角的余角相等求出∠BCE=∠E,根据等角对等边可得BC=BE,然后表示出AD、AE,再利用根与系数的关系表示出AD+AE,AD•AE,根据勾股定理可得b2=c2-a2,整理后写出方程即可.
解答:解:设BC=a,
∵BD=BC,
∴∠BDC=∠BCD,
∵CE⊥CD,
∴∠BCE+∠BCD=∠E+∠BDC=90°,
∴∠BCE=∠E,
∴BC=BE=a,
∵AC=b,AB=c,
∴AD=AB-BD=c-a,
AE=AB+BE=c+a,
∴AD+AE=c-a+c+a=2c,
AD•AE=(c-a)(c+a)=c2-a2,
由勾股定理得,b2=c2-a2,
∴AD•AE=b2,
∴以AD和AE的长为根的一元二次方程是x2-2cx+b2=0.
故答案为:x2-2cx+b2=0.
∵BD=BC,
∴∠BDC=∠BCD,
∵CE⊥CD,
∴∠BCE+∠BCD=∠E+∠BDC=90°,
∴∠BCE=∠E,
∴BC=BE=a,
∵AC=b,AB=c,
∴AD=AB-BD=c-a,
AE=AB+BE=c+a,
∴AD+AE=c-a+c+a=2c,
AD•AE=(c-a)(c+a)=c2-a2,
由勾股定理得,b2=c2-a2,
∴AD•AE=b2,
∴以AD和AE的长为根的一元二次方程是x2-2cx+b2=0.
故答案为:x2-2cx+b2=0.
点评:本题考查了勾股定理,等边对等角的性质,等角对等边的性质,用a、c表示出AD、AE是解题的关键,也是本题的难点.

练习册系列答案
相关题目
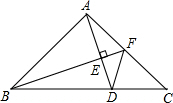 已知△ABC,AB=AC,∠BAC=90°,点F在AC上,BF⊥AD垂足为E.若DE=2,∠AFB=∠CFD,则△ADF的面积为
已知△ABC,AB=AC,∠BAC=90°,点F在AC上,BF⊥AD垂足为E.若DE=2,∠AFB=∠CFD,则△ADF的面积为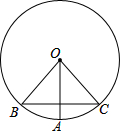 如图,在⊙O中,OA⊥BC于G,已知BC=2,OA=2,则∠BOA=
如图,在⊙O中,OA⊥BC于G,已知BC=2,OA=2,则∠BOA=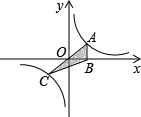 如图,正比例函数y=x与反比例函数y=
如图,正比例函数y=x与反比例函数y=