题目内容
 某校兴趣小组坐游轮拍摄瓯江两岸美景.如图,游轮出发点A与江心屿B的距离为300m.在一处测得江心屿B位于A的北偏东30°方向.游轮沿正北方向行驶一段时间后到达C.在C处测得江心屿B位于C的北偏东60°方向.求此时游轮与江心屿之间的距离BC (结果保留整数).
某校兴趣小组坐游轮拍摄瓯江两岸美景.如图,游轮出发点A与江心屿B的距离为300m.在一处测得江心屿B位于A的北偏东30°方向.游轮沿正北方向行驶一段时间后到达C.在C处测得江心屿B位于C的北偏东60°方向.求此时游轮与江心屿之间的距离BC (结果保留整数).考点:解直角三角形的应用-方向角问题
专题:
分析:首先利用三角形的外角的性质求得∠B的度数,证明△ABC是等腰三角形,根据三线合一定理即可求得BE的长,然后根据三角函数即可求得BC的长.
解答: 解:作CE⊥AB于点E.
解:作CE⊥AB于点E.
∵∠BCD=∠A+∠B,
∴∠B=∠BCD-∠A=60°-30°=30°,
∴∠A=∠B,
∴BC=AC,
∵CE⊥AB
∴BE=
AB=
×300=150(m).
在直角△BCE中,BC=
=
=100
≈173(m).
答:此时游轮与江心屿之间的距离BC约是173m.
 解:作CE⊥AB于点E.
解:作CE⊥AB于点E.∵∠BCD=∠A+∠B,
∴∠B=∠BCD-∠A=60°-30°=30°,
∴∠A=∠B,
∴BC=AC,
∵CE⊥AB
∴BE=
| 1 |
| 2 |
| 1 |
| 2 |
在直角△BCE中,BC=
| BE |
| cos30° |
| 150 | ||||
|
| 3 |
答:此时游轮与江心屿之间的距离BC约是173m.
点评:本题考查了方向角的定义,依据直角三角形的性质,正确证明△ABC是等腰三角形是关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 如图,半径为5的圆O中,弦AB的长为8,则圆心O到弦AB的距离为( )
如图,半径为5的圆O中,弦AB的长为8,则圆心O到弦AB的距离为( )| A、3 | B、4 | C、5 | D、6 |
已知抛物线y=x2+ax+b与x轴的两个不同的交点A.B距离原点都大于1且小于2,一个直角三角形的两条直角边长分别为a.b,则斜边c的取值范围是( )
| A、4<c<25 | ||||
| B、2<c<5 | ||||
| C、5<c<32 | ||||
D、
|
实数-2,
,
,-0.3,sin30°,π,0.1010010001,中无理数的个数是( )
| ||
| 2 |
| 22 |
| 7 |
| A、1个 | B、2个. | C、3个 | D、4个 |
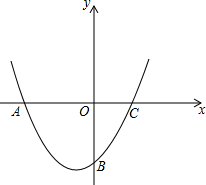 如图在平面直角坐标系中,已知抛物线
如图在平面直角坐标系中,已知抛物线 如图,在四边形ABCD中,∠BAD=∠BCD=90°,点O是BD的中点,且OA=5cm,那么OC的长等于
如图,在四边形ABCD中,∠BAD=∠BCD=90°,点O是BD的中点,且OA=5cm,那么OC的长等于