题目内容
13.二次函数y=-$\frac{1}{2}$x2+x+4的图象与x轴的交点从右向左为A,B两点,与y轴的交点为C,顶点D.(1)求四边形ABCD的面积;
(2)在第一象限内的抛物线上求一点D′,使四边形ABCD′的面积最大.
分析 (1)连接OD,当y=0时,-$\frac{1}{2}$x2+x+4=0,解方程得出x=4,或x=-2,得出点A和B的坐标,当x=0时,y=4,得出点C的坐标,把二次函数化成顶点式,得出顶点坐标,四边形ABCD的面积=△BOC的面积+△OCD的面积+△OAD的面积,即可得出结果;
(2)设D′(x,-$\frac{1}{2}$x2+x+4),四边形ABCD′的面积为S,则四边形ABCD′的面积S=△BOC的面积+△OCD′的面积+△OAD′的面积,得出S是x的二次函数,得出当x=2时,S最大,当x=2时,求出纵坐标即可.
解答 解:(1) 如图所示:连接OD,
如图所示:连接OD,
∵二次函数y=-$\frac{1}{2}$x2+x+4,
当y=0时,-$\frac{1}{2}$x2+x+4=0,
解得:x=4,或x=-2,
∴A(4,0),B(-2,0);
当x=0时,y=4,
∴C(0,4),
∵二次函数y=-$\frac{1}{2}$x2+x+4=-$\frac{1}{2}$(x-1)2+$\frac{9}{2}$,
∴D(1,$\frac{9}{2}$),
∴四边形ABCD的面积=△BOC的面积+△OCD的面积+△OAD的面积=$\frac{1}{2}$×2×4+$\frac{1}{2}$×4×1+$\frac{1}{2}$×4×$\frac{9}{2}$=15;
(2)如图2所示:
设D′(x,-$\frac{1}{2}$x2+x+4),四边形ABCD′的面积为S,
则四边形ABCD′的面积S=△BOC的面积+△OCD′的面积+△OAD′的面积
=$\frac{1}{2}$×2×4+$\frac{1}{2}$×4×x+$\frac{1}{2}$×4×(-$\frac{1}{2}$x2+x+4)
=-x2+4x+12
=-(x-2)2+16,
∵-1<0,
∴S有最大值,当x=2时,S最大,
当x=2时,-$\frac{1}{2}$x2+x+4=4,
∴D′坐标为(2,4).
点评 本题考查了抛物线与坐标轴的交点坐标、二次函数的综合运用以及最值问题;熟练掌握二次函数的运用,求出抛物线与坐标轴的交点坐标是解决问题的关键.

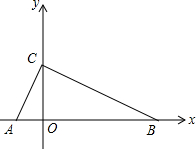 如图,已知Rt△ABC的斜边AB在x轴上,斜边上的高CO在y轴的正半轴上,且OA=1,OC=2,求经过A、B、C三点的二次函数解析式.
如图,已知Rt△ABC的斜边AB在x轴上,斜边上的高CO在y轴的正半轴上,且OA=1,OC=2,求经过A、B、C三点的二次函数解析式. 甲、乙两村与公路AC、BD的相对位置如图所示.现要设立一个医疗站点P,使其满足下列条件:①到公路OA、OB的距离相等;②到甲、乙两村的距离也相等.请确定点P的位置(用直尺和圆规作图,保留作图痕迹).
甲、乙两村与公路AC、BD的相对位置如图所示.现要设立一个医疗站点P,使其满足下列条件:①到公路OA、OB的距离相等;②到甲、乙两村的距离也相等.请确定点P的位置(用直尺和圆规作图,保留作图痕迹).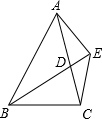 如图,BD为△ABC的角平分线,且BD=BC,E为BD延长线上的一点,BE=BA.则下列结论正确的是:①△ABD≌△EBC;②S△ABD=S△BDC;③∠BCE+∠BCD=180°;④AD=AE=EC;其中正确的是( )
如图,BD为△ABC的角平分线,且BD=BC,E为BD延长线上的一点,BE=BA.则下列结论正确的是:①△ABD≌△EBC;②S△ABD=S△BDC;③∠BCE+∠BCD=180°;④AD=AE=EC;其中正确的是( ) 如图,AB=AC,BD=DC,∠BDC=110°,求∠ADB的度数.
如图,AB=AC,BD=DC,∠BDC=110°,求∠ADB的度数.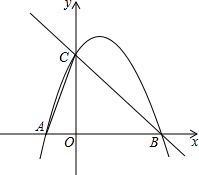 如图,己知抛物线与x轴分别交于A(-1,0)、B(3,0)两点,与y轴交于点C(0,3).
如图,己知抛物线与x轴分别交于A(-1,0)、B(3,0)两点,与y轴交于点C(0,3).