题目内容
如图，AB是⊙O的直径，CD为弦，CD⊥AB于点E，CD=16cm，BE=4cm，求⊙O的半径．考点：垂径定理,勾股定理
专题：计算题
分析：连结OC，设圆的半径为R，根据垂径定理得CE=
CD=8，然后在Rt△OCE中，根据勾股定理得到R2=（R-4）2+82，再解方程即可．
| 1 |
| 2 |
解答：
解：连结OC，如图，设圆的半径为R，
∵AB是⊙O的直径，CD为弦，CD⊥AB于点E，
∴CE=DE=
CD=
×16=8，
在Rt△OCE中，OC=R，OE=OB-BE=R-4，CE=8，
∴R2=（R-4）2+82，解得R=10，
即⊙O的半径为10cm．
解：连结OC，如图，设圆的半径为R，∵AB是⊙O的直径，CD为弦，CD⊥AB于点E，
∴CE=DE=
| 1 |
| 2 |
| 1 |
| 2 |
在Rt△OCE中，OC=R，OE=OB-BE=R-4，CE=8，
∴R2=（R-4）2+82，解得R=10，
即⊙O的半径为10cm．
点评：本题考查了垂径定理：平分弦的直径平分这条弦，并且平分弦所对的两条弧．也考查了勾股定理．
练习册系列答案
相关题目
2014年1月10日，绿色和平发布了全国74个城市PM2.5浓度年均值排名和相应的最大日均值，其中浙江省六个地区的浓度如图（舟山的最大日均值条形图缺损）以下说法中错误的是（ ）| A、这6个地区中，最大日均值最高的是绍兴 |
| B、杭州的年均值约是舟山的2倍 |
| C、舟山的最大日均值不一定低于丽水的最大日均值 |
| D、这6个地区中，低于国家环境空气质量标准规定的年均值35微克每立方米的地区只有舟山 |
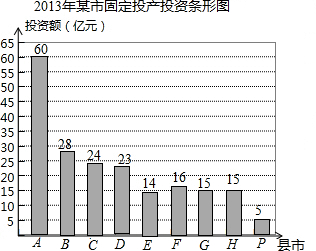某地统计局对2013年各县市的固定资产投资情况进行了统计，并绘成了如图，请根据相关信息解答下列问题：下列结论不正确的是（ ）| A、2013年某市固定资产投资总额为200亿元 |
| B、2013年某市各单位固定资产投资额的中位数是16亿元 |
| C、2013年A县固定资产投资额为占总额的30% |
| D、2013年固定资产投资扇形统计图中表示A地的扇形的圆心角为110° |
