题目内容
7.已知三角形的周长为13,三边长a、b、c都是整数,且满足a≤b≤c,那么满足条件的三角形有多少个?分别求出来.分析 三角形的边长均为正整数,且周长等于13,根据在三角形中任意两边之和大于第三边,任意两边之差小于第三边.根据不等式即可求解.
解答 解:$\left\{\begin{array}{l}{a+b+c=13}\\{c<a+b}\\{c≥\frac{13}{3}}\end{array}\right.$
解得$\frac{13}{3}$≤c<$\frac{13}{2}$,由于最长的边为c,且c为整数,所以c=5或c=6;
当c=5时,有$\left\{\begin{array}{l}{a+b=8}\\{a≤b}\\{b≤5}\end{array}\right.$,解得4≤b≤5,又边都为整数,则$\left\{\begin{array}{l}{a=4}\\{b=4}\end{array}\right.$或$\left\{\begin{array}{l}{a=3}\\{b=5}\end{array}\right.$;
当c=6时,有$\left\{\begin{array}{l}{a+b=7}\\{a≤b}\\{b≤6}\end{array}\right.$,解得$\frac{7}{2}$≤b≤6,同理的整数解$\left\{\begin{array}{l}{a=3}\\{b=4}\end{array}\right.$或$\left\{\begin{array}{l}{a=2}\\{b=5}\end{array}\right.$或$\left\{\begin{array}{l}{a=1}\\{b=6}\end{array}\right.$;
综上:满足条件的三角形有5个,三边长分别为$\left\{\begin{array}{l}{a=4}\\{b=4}\\{c=5}\end{array}\right.$、$\left\{\begin{array}{l}{a=3}\\{b=5}\\{c=5}\end{array}\right.$、$\left\{\begin{array}{l}{a=3}\\{b=4}\\{c=6}\end{array}\right.$、$\left\{\begin{array}{l}{a=2}\\{b=5}\\{c=6}\end{array}\right.$、$\left\{\begin{array}{l}{a=1}\\{b=6}\\{c=6}\end{array}\right.$
点评 本题考查了三角形的三边关系,利用了三角形中三边的关系求解.注意分类讨论,不重不漏.

 如图,在△ABC中,∠A=90°,BD是角平分线,若AB=8,BC=10,S△ABD=$\frac{32}{3}$,求△BDC的面积.
如图,在△ABC中,∠A=90°,BD是角平分线,若AB=8,BC=10,S△ABD=$\frac{32}{3}$,求△BDC的面积.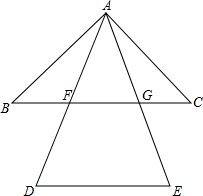 如图,已知△ABC和△ADE都是等腰三角形,AB=AC,AD=AE且∠DAB=∠EAC,则DE∥BC吗?为什么?
如图,已知△ABC和△ADE都是等腰三角形,AB=AC,AD=AE且∠DAB=∠EAC,则DE∥BC吗?为什么?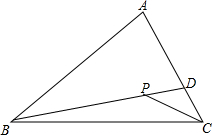 已知在三角形ABC中,存在一点P,连接PB、PC,延长BP交AC于点D,求证:AB+AC>PB+PC.
已知在三角形ABC中,存在一点P,连接PB、PC,延长BP交AC于点D,求证:AB+AC>PB+PC.
 某校为了了解八年级学生的身体发育情况,从全体八年级的学生中抽取了一些学生进行身高测量,所得数据如图,则该校的八年级学生的平均身高为162cm.
某校为了了解八年级学生的身体发育情况,从全体八年级的学生中抽取了一些学生进行身高测量,所得数据如图,则该校的八年级学生的平均身高为162cm.