题目内容
19. 如图,∠AOB=90°,将三角尺的直角顶点落在∠AOB的角平分线OC的任意一点P上,使三角尺的两条直角边与∠AOB的两边分别相交于点E、F,求证:PE=PF.
如图,∠AOB=90°,将三角尺的直角顶点落在∠AOB的角平分线OC的任意一点P上,使三角尺的两条直角边与∠AOB的两边分别相交于点E、F,求证:PE=PF.
分析 过点P作PM⊥OA于M,PN⊥⊥OB于N,根据角平分线的性质:角平分线上的点到这个角两边的距离相等,PM=PN,可以通过证明PM、PN所两在的两个直角三角形全等,即Rt△PEM≌Rt△PFM 来证明PE=PF
解答 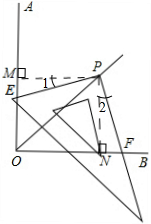 证明:过点P作PM⊥OA于M,PN⊥⊥OB于N,则∠PMO=∠PNO=90°
证明:过点P作PM⊥OA于M,PN⊥⊥OB于N,则∠PMO=∠PNO=90°
∵∠AOB=90°
∴四边形OMPN是矩形(有三个角是直角的四边形是矩形)
∴∠MPN=90°(矩形的四个角都是直角)
又∵∠EPF=90°(已知)
∴∠MPN=∠EPF,
∴∠MPN-∠EPN=∠EPF-∠EPN
即:∠1=∠2
∵OP平分∠AOB(已知)
∴PM=PN(角平分线上的点到这个角两边的距离相等)
∴△PME≌△PNF(AAS)
∴PE=PF(全等三角形的对应边相等)
点评 本题是证明两条线段相等.证明两条线段相等,通常是证明这两条线段所在的三角形全等,然后再根据全等三角形对应边相等证得的结论.注意题目给出了角平分线,常常应用到角平分线性质构造辅助线帮助解决问题.

练习册系列答案
 培优好卷单元加期末卷系列答案
培优好卷单元加期末卷系列答案
相关题目
9.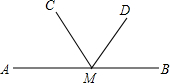 如图,已知点M是直线AB上一点,∠AMC=52°48′,∠BMD=72°19°,则∠CMD等于( )
如图,已知点M是直线AB上一点,∠AMC=52°48′,∠BMD=72°19°,则∠CMD等于( )
 如图,已知点M是直线AB上一点,∠AMC=52°48′,∠BMD=72°19°,则∠CMD等于( )
如图,已知点M是直线AB上一点,∠AMC=52°48′,∠BMD=72°19°,则∠CMD等于( )| A. | 49°07′ | B. | 54°53′ | C. | 55°53′ | D. | 53°7′ |
 已知:如图,在正方形ABCD外取一点E,连接AE、BE、DE,过点A作AE的垂线交DE于点P.若AE=AP=1,PB=$\sqrt{5}$,下列结论:①△APD≌△AEB;②点B到直线AE的距离为$\sqrt{2}$;③EB⊥ED;④S△APD+S△APB=$\frac{1+\sqrt{6}}{2}$.其中正确结论的序号是①③④.
已知:如图,在正方形ABCD外取一点E,连接AE、BE、DE,过点A作AE的垂线交DE于点P.若AE=AP=1,PB=$\sqrt{5}$,下列结论:①△APD≌△AEB;②点B到直线AE的距离为$\sqrt{2}$;③EB⊥ED;④S△APD+S△APB=$\frac{1+\sqrt{6}}{2}$.其中正确结论的序号是①③④.

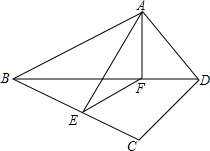 已知:四边形ABCD中,AD=CD,对角线BD平分∠ADC,点E,F分别是线段BC和线段BD上的点,且点F在线段EC的垂直平分线上,连接EF,AF,AE.
已知:四边形ABCD中,AD=CD,对角线BD平分∠ADC,点E,F分别是线段BC和线段BD上的点,且点F在线段EC的垂直平分线上,连接EF,AF,AE. 两个全等的正十二边形按如图所示的方式摆放,其中两顶点重合,则∠α=60度.
两个全等的正十二边形按如图所示的方式摆放,其中两顶点重合,则∠α=60度.