题目内容
4.(1)如图①,D是△ABC的边AB上一点,DF交AC于点E,DE=EF,FC∥AB,求证:AB-CF=BD;(2)如图②,在△ABC中,AD、BE分别是BC、AC边上的高,EB、AD的延长线交于点H,且AC=BH.求证:∠ABC=135°.

分析 (1)根据平行线性质求出∠A=∠FCE,根据AAS推出△ADE≌△CFE,利用全等三角形的性质可得AD=CF,等量代换即可;
(2)首先求出∠H=∠C,进而在△ADC和△BDH中利用AAS证明△ADC≌△BDH,即可得到AD=DB,于是得到△ADB是等腰直角三角形,即可证明结论.
解答 证明:(1)∵FC∥AB,
∴∠A=∠FCE,
在△ADE和△CFE中,
$\left\{\begin{array}{l}{∠AED=∠FEC}\\{∠A=∠FCE}\\{DE=EF}\end{array}\right.$,
∴△ADE≌△CFE(AAS),
∴AD=CF,
∵AB-AD=BD,
∴AB-CF=BD;
(2)∵HE⊥AC,
∴在Rt△AEH中,∠H+∠HAE=90°,
∵AD⊥DC,
∴在Rt△ADC中,∠C+∠HAE=90°,
∴∠H=∠C,
在△ADC和△BDH中,
∵$\left\{\begin{array}{l}{∠C=∠H}\\{∠ADC=∠BDH=90°}\\{AC=BH}\end{array}\right.$,
∴△ADC≌△BDH(AAS),
∴AD=DB,
∴△ADB是等腰直角三角形,
∴∠ABD=45°,
∴∠ABC=180°-45°=135°.
点评 本题主要考查了全等三角形的判定与性质的知识,解答本题的关键是掌握AAS证明两三角形全等,此题难度不大.

练习册系列答案
相关题目
 在数学课上,许老师在黑板上画出如图所示的图形(其中B、F、C、E在同一条直线上),并写出四个条件:
在数学课上,许老师在黑板上画出如图所示的图形(其中B、F、C、E在同一条直线上),并写出四个条件: 如图,半径为1的⊙O与正五边形ABCDE相切于点A、C,则劣弧$\widehat{AC}$的长度为$\frac{4π}{5}$.
如图,半径为1的⊙O与正五边形ABCDE相切于点A、C,则劣弧$\widehat{AC}$的长度为$\frac{4π}{5}$. 如图,∠AOB=90°,将三角尺的直角顶点落在∠AOB的角平分线OC的任意一点P上,使三角尺的两条直角边与∠AOB的两边分别相交于点E、F,求证:PE=PF.
如图,∠AOB=90°,将三角尺的直角顶点落在∠AOB的角平分线OC的任意一点P上,使三角尺的两条直角边与∠AOB的两边分别相交于点E、F,求证:PE=PF.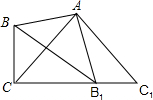 如图所示,∠BAB1=∠CAC1=90°,AB=AB1,AC=AC1,B1在CC1上.
如图所示,∠BAB1=∠CAC1=90°,AB=AB1,AC=AC1,B1在CC1上.
 如图所示,已知AD是Rt△ABC的斜边BC上的高,E为AC上一点,连接BE交AD于点F,若AE=AF,求证:BE平分∠ABC.
如图所示,已知AD是Rt△ABC的斜边BC上的高,E为AC上一点,连接BE交AD于点F,若AE=AF,求证:BE平分∠ABC.