题目内容
11.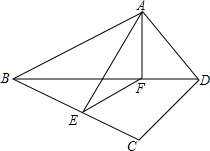 已知:四边形ABCD中,AD=CD,对角线BD平分∠ADC,点E,F分别是线段BC和线段BD上的点,且点F在线段EC的垂直平分线上,连接EF,AF,AE.
已知:四边形ABCD中,AD=CD,对角线BD平分∠ADC,点E,F分别是线段BC和线段BD上的点,且点F在线段EC的垂直平分线上,连接EF,AF,AE.(1)求证:AF=EF;
(2)求证:∠EAF=∠ABD.
分析 (1)由△ADF≌△CDF得AF=CF,又点F在线段EC的垂直平分线上得EF=C即可证明.
(2)先证明∠FEC=∠BAF得A、B、E、F四点共圆故∠EAF=∠EBH=∠ABD.
解答 (1)证明:如图,连接CF.
∵BD平分∠ADC,
∴∠ADB=∠CDB,
在△ADF和△CDF中,
$\left\{\begin{array}{l}{AD=DC}\\{∠ADF=∠CDF}\\{DF=DF}\end{array}\right.$,
∴△ADF≌△CDF,
∴AF=CF,
∵点F在线段EC的垂直平分线上,
∴EF=CF,
∴AF=EF.
(2)证明:∵BD平分∠ADC,
∴∠ADB=∠CDB
在△ADB和△CDB中,
$\left\{\begin{array}{l}{AD=CD}\\{∠ADB=∠CDB}\\{BD=BD}\end{array}\right.$,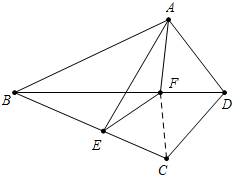
∴△ADB≌△CDB,
∴∠ABD=∠CBD,AB=BC,
在△BAF和△BCF中,
$\left\{\begin{array}{l}{AB=BC}\\{∠ABF=∠CBF}\\{BF=BF}\end{array}\right.$,
∴△BFA≌△BFC,
∴∠BAF=∠BCF,
∵FE=FC,
∴∠FEC=∠FCE,
∴∠FEC=∠BAF,
∴A、B、E、F四点共圆,
∴∠EAF=∠EBH=∠ABD.
点评 本题考查全等三角形的判定和性质、垂直平分线的性质、四点共圆等知识,充分利用三角形全等是解决问题的关键.

练习册系列答案
相关题目
11.“十年树木,百年树人”,教师的素养关系到国家的未来.我区招聘音乐教师采用笔试、专业技能测试、说课三种形式进行选拔,这三项的成绩满分均为100分,并分别按2:3:5的比例折算总分,最后,按照折算后成绩的排序从高到低依次录取.该区要招聘2名音乐教师,而参与的6名选手的各项成绩见下表:
(1)笔试成绩的极差是多少?
(2)写出说课成绩的中位数、众数;
(3)已知序号为1,2,3,4,5号选手的成绩已经折算出,分别为84.2分,84.6分,88.1分,80.8分,86.4分,请计算6号选手的成绩,并判断这六位选手中序号是多少的选手将被录用?为什么?
| 序号 | 1 | 2 | 3 | 4 | 5 | 6 |
| 笔试成绩 | 66 | 90 | 86 | 64 | 65 | 84 |
| 专业技能测试成绩 | 95 | 92 | 93 | 80 | 88 | 92 |
| 说课成绩 | 85 | 78 | 86 | 88 | 94 | 85 |
(2)写出说课成绩的中位数、众数;
(3)已知序号为1,2,3,4,5号选手的成绩已经折算出,分别为84.2分,84.6分,88.1分,80.8分,86.4分,请计算6号选手的成绩,并判断这六位选手中序号是多少的选手将被录用?为什么?
2. 如图,点P是正方形ABCD的对角线BD上的一个动点(不与B、D重合),连结AP,过点B作直线AP的垂线,垂足为H,连结DH.若正方形的边长为4,则线段DH长度的最小值是2$\sqrt{5}$-2.
如图,点P是正方形ABCD的对角线BD上的一个动点(不与B、D重合),连结AP,过点B作直线AP的垂线,垂足为H,连结DH.若正方形的边长为4,则线段DH长度的最小值是2$\sqrt{5}$-2.
 如图,点P是正方形ABCD的对角线BD上的一个动点(不与B、D重合),连结AP,过点B作直线AP的垂线,垂足为H,连结DH.若正方形的边长为4,则线段DH长度的最小值是2$\sqrt{5}$-2.
如图,点P是正方形ABCD的对角线BD上的一个动点(不与B、D重合),连结AP,过点B作直线AP的垂线,垂足为H,连结DH.若正方形的边长为4,则线段DH长度的最小值是2$\sqrt{5}$-2.
1.(-2)-1的值是( )
| A. | 2 | B. | $\frac{1}{2}$ | C. | $-\frac{1}{5}$ | D. | $-\frac{1}{2}$ |
 如图,∠AOB=90°,将三角尺的直角顶点落在∠AOB的角平分线OC的任意一点P上,使三角尺的两条直角边与∠AOB的两边分别相交于点E、F,求证:PE=PF.
如图,∠AOB=90°,将三角尺的直角顶点落在∠AOB的角平分线OC的任意一点P上,使三角尺的两条直角边与∠AOB的两边分别相交于点E、F,求证:PE=PF. 如图所示,在△ABC中,D是BC延长线上一点,CD=BC,E是CA延长线上一点,AE=2AC,若AD=BE,求证:△ABC是直角三角形.
如图所示,在△ABC中,D是BC延长线上一点,CD=BC,E是CA延长线上一点,AE=2AC,若AD=BE,求证:△ABC是直角三角形.
 已知数轴上A、B两点对应数分别为-2和4,P为数轴上一动点,对应数为x.
已知数轴上A、B两点对应数分别为-2和4,P为数轴上一动点,对应数为x.