题目内容
7.计算:$\frac{201{7}^{2}}{201{6}^{2}+201{8}^{2}-2}$=$\frac{1}{2}$.分析 将算式变形为$\frac{201{7}^{2}}{(2017-1)^{2}+(2017+1)^{2}-2}$,根据完全平方公式得到原式=$\frac{201{7}^{2}}{201{7}^{2}-2017×2+1+201{7}^{2}+2017×2+1-2}$,再化简后约分即可求解.
解答 解:$\frac{201{7}^{2}}{201{6}^{2}+201{8}^{2}-2}$
=$\frac{201{7}^{2}}{(2017-1)^{2}+(2017+1)^{2}-2}$
=$\frac{201{7}^{2}}{201{7}^{2}-2017×2+1+201{7}^{2}+2017×2+1-2}$
=$\frac{201{7}^{2}}{2×201{7}^{2}}$
=$\frac{1}{2}$.
故答案为:$\frac{1}{2}$.
点评 考查了完全平方公式,解题的关键是将算式变形为$\frac{201{7}^{2}}{(2017-1)^{2}+(2017+1)^{2}-2}$.

练习册系列答案
 期末冲刺100分创新金卷完全试卷系列答案
期末冲刺100分创新金卷完全试卷系列答案
相关题目
3.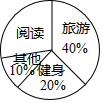 某企业为了解职工业余爱好,组织对本企业150名职工业余爱好进行调查,制成了如图所示的扇形统计图,则在被调查的职工中,爱好旅游和阅读的人数分别是( )
某企业为了解职工业余爱好,组织对本企业150名职工业余爱好进行调查,制成了如图所示的扇形统计图,则在被调查的职工中,爱好旅游和阅读的人数分别是( )
 某企业为了解职工业余爱好,组织对本企业150名职工业余爱好进行调查,制成了如图所示的扇形统计图,则在被调查的职工中,爱好旅游和阅读的人数分别是( )
某企业为了解职工业余爱好,组织对本企业150名职工业余爱好进行调查,制成了如图所示的扇形统计图,则在被调查的职工中,爱好旅游和阅读的人数分别是( )| A. | 45,30 | B. | 60,40 | C. | 60,45 | D. | 40,45 |
19. 如图,AD∥BC,AD⊥AB,点A,B在y轴上,CD与x轴交于点E(2,0),且AD=DE,BC=2CE,则BD与x轴交点F的横坐标为( )
如图,AD∥BC,AD⊥AB,点A,B在y轴上,CD与x轴交于点E(2,0),且AD=DE,BC=2CE,则BD与x轴交点F的横坐标为( )
 如图,AD∥BC,AD⊥AB,点A,B在y轴上,CD与x轴交于点E(2,0),且AD=DE,BC=2CE,则BD与x轴交点F的横坐标为( )
如图,AD∥BC,AD⊥AB,点A,B在y轴上,CD与x轴交于点E(2,0),且AD=DE,BC=2CE,则BD与x轴交点F的横坐标为( )| A. | $\frac{2}{3}$ | B. | $\frac{3}{4}$ | C. | $\frac{4}{5}$ | D. | $\frac{5}{6}$ |
16.如果关于x的方程ax2+4x-3=0有两个实数根,且关于x的分式方程$\frac{x}{x-3}$$+\frac{a-2}{3-x}$=a有整数解,则符合条件的整数a有( )个.
| A. | 3 | B. | 4 | C. | 5 | D. | 6 |
17.一架25分米长的梯子,斜立在一竖直的墙上,这时梯足距离墙底端7分米.如果梯子的顶端沿墙下滑4分米,那么梯足将滑动( )
| A. | 9分米 | B. | 15分米 | C. | 5分米 | D. | 8分米 |
 如图,FG为⊙O的直径,$\widehat{HF}$=$\widehat{HG}$,E为$\widehat{HF}$上一点,延长FE至点A,使EA=EG,连接HG.
如图,FG为⊙O的直径,$\widehat{HF}$=$\widehat{HG}$,E为$\widehat{HF}$上一点,延长FE至点A,使EA=EG,连接HG. 如图,用若干个全等的正五边形可以拼成一个环状,图中所示的是前3个正五边形的拼接情况,要完全拼成一个圆环共需要的正五边形个数是( )
如图,用若干个全等的正五边形可以拼成一个环状,图中所示的是前3个正五边形的拼接情况,要完全拼成一个圆环共需要的正五边形个数是( )