题目内容
19. 如图,AD∥BC,AD⊥AB,点A,B在y轴上,CD与x轴交于点E(2,0),且AD=DE,BC=2CE,则BD与x轴交点F的横坐标为( )
如图,AD∥BC,AD⊥AB,点A,B在y轴上,CD与x轴交于点E(2,0),且AD=DE,BC=2CE,则BD与x轴交点F的横坐标为( )| A. | $\frac{2}{3}$ | B. | $\frac{3}{4}$ | C. | $\frac{4}{5}$ | D. | $\frac{5}{6}$ |
分析 如图,设OF=a,AD=DE=x,CE=y,则BC=2y,根据平行线分线段成比例可得xy=a(x+y),2xy=(2-a)(x+y),联立得到2a(x+y)=(2-a)(x+y)且x+y≠0,即2a=(2-a),解方程求得a,从而求解.
解答 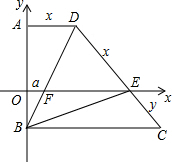 解:如图,设OF=a,AD=DE=x,CE=y,则BC=2y,
解:如图,设OF=a,AD=DE=x,CE=y,则BC=2y,
则$\frac{OF}{AD}$=$\frac{BF}{BD}$=$\frac{EC}{CD}$,
即$\frac{a}{x}$=$\frac{y}{x+y}$,
xy=a(x+y),
又∵$\frac{EF}{BC}$=$\frac{DE}{CD}$,即$\frac{2-a}{2y}$=$\frac{x}{x+y}$,
2xy=(2-a)(x+y),
∴2a(x+y)=(2-a)(x+y)且x+y≠0,
∴2a=(2-a),
解得a=$\frac{2}{3}$.
故点F的横坐标为$\frac{2}{3}$.
故选:A.
点评 考查了坐标与图形性质,平行线分线段成比例,关键是熟练掌握平行线分线段成比例的性质,注意方程思想的运用.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
10.掷一枚均匀的正六面体骰子,前5次朝上的点数恰好是1~5,则第6次朝上的点数是6的可能性( )
| A. | 等于朝上点数为5的可能性 | B. | 大于朝上点数为5的可能性 | ||
| C. | 小于朝上点数为5的可能性 | D. | 无法确定 |
4.把20克糖溶解在80克水中,糖水的含糖率是( )
| A. | 20% | B. | 80% | C. | 100% | D. | 无法计算 |
 如图所示,已知∠AOC=∠BOD=75°,∠BOC=30°,求∠AOD的度数.
如图所示,已知∠AOC=∠BOD=75°,∠BOC=30°,求∠AOD的度数.