题目内容
15.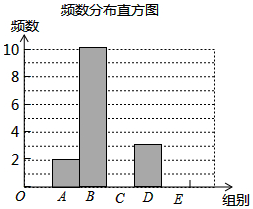 在一次社会调查活动中,小华收集到某“健步走运动”团队中一些成员一天行走的步数,并对这些数据按组距1000进行分组,并统计整理,绘制了如下尚不完整的统计图表:
在一次社会调查活动中,小华收集到某“健步走运动”团队中一些成员一天行走的步数,并对这些数据按组距1000进行分组,并统计整理,绘制了如下尚不完整的统计图表:| 组别 | 步数分组 | 频数 | 频率 |
| A | 5500≤x<6500 | 2 | 0.10 |
| B | 6500≤x<7500 | 10 | 0.50 |
| C | 7500≤x<8500 | a | m |
| D | 8500≤x<9500 | 3 | 0.05 |
| E | 9500≤x<10500 | b | 0.05 |
| 合计 | 5500≤x<10500 | c | 1 |
(1)填空:a=6,c=20,m=0.3;
(2)补全频数分布直方图;
(3)若该团队共有200人,请估计其中一天行走步数不少于7500步的人数.
分析 (1)根据百分比=$\frac{所占人数}{总人数}$,频率之和等于1等知识,一一解答即可.
(2)根据a、b的值画出条形图即可;
(3)利用样本估计总体的思想思考问题即可;
解答 解:(1)c=2÷0.1=20,b=20×0.05=1,m=1-0.1-0.5-0.05-0.05=0.3,
a=20×0.3=6,
故答案分别为6,20,0.3.
(2)条形图如图所示:
(3)200×$\frac{10}{20}$=100人,
答:若该团队共有200人,请估计其中一天行走步数不少于7500步的人数为100人.
点评 本题考查频数分布直方图、频数分布表、样本估计总体的思想等知识,解题的关键是灵活运用所学知识解决问题,属于中考常考题型.

练习册系列答案
相关题目
5. 如图所示,直线AB、CD相交于点O,且∠AOD+∠BOC=110°,则∠AOC的度数是( )
如图所示,直线AB、CD相交于点O,且∠AOD+∠BOC=110°,则∠AOC的度数是( )
 如图所示,直线AB、CD相交于点O,且∠AOD+∠BOC=110°,则∠AOC的度数是( )
如图所示,直线AB、CD相交于点O,且∠AOD+∠BOC=110°,则∠AOC的度数是( )| A. | 110° | B. | 115° | C. | 120° | D. | 125° |
10. 如图直线a∥b,若∠1=70°,则∠2为( )
如图直线a∥b,若∠1=70°,则∠2为( )
 如图直线a∥b,若∠1=70°,则∠2为( )
如图直线a∥b,若∠1=70°,则∠2为( )| A. | 70° | B. | 110° | C. | 70°或110° | D. | 120° |
20. 如图,EF∥MN,AC,BD交于点O,且分别平分∠FAB,∠ABN,图中与∠1互余的角有( )
如图,EF∥MN,AC,BD交于点O,且分别平分∠FAB,∠ABN,图中与∠1互余的角有( )
 如图,EF∥MN,AC,BD交于点O,且分别平分∠FAB,∠ABN,图中与∠1互余的角有( )
如图,EF∥MN,AC,BD交于点O,且分别平分∠FAB,∠ABN,图中与∠1互余的角有( )| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
7. 如图,点D在△ABC边BC的延长线上,BA=BC,DB=DA,若∠BAC=m,∠ADB=n,则m与n之间的关系是( )
如图,点D在△ABC边BC的延长线上,BA=BC,DB=DA,若∠BAC=m,∠ADB=n,则m与n之间的关系是( )
 如图,点D在△ABC边BC的延长线上,BA=BC,DB=DA,若∠BAC=m,∠ADB=n,则m与n之间的关系是( )
如图,点D在△ABC边BC的延长线上,BA=BC,DB=DA,若∠BAC=m,∠ADB=n,则m与n之间的关系是( )| A. | 3m+n=180° | B. | 4m-n=180° | C. | 3m-n=180° | D. | 2m+n=180° |
4.阿信、小怡两人打算搭乘同一班次电车上学,若此班次电车共有5节车厢,且阿信从任意一节车厢上车的机会相等,小怡从任意一节车厢上车的机会相等,则两人从同一节车厢上车的概率为何( )
| A. | $\frac{1}{2}$ | B. | $\frac{1}{5}$ | C. | $\frac{1}{10}$ | D. | $\frac{1}{25}$ |
5.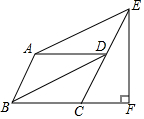 如图,在?ABCD中,∠BAD=120°,连接BD,作AE∥BD交CD延长线于点E,过点E作EF⊥BC交BC的延长线于点F,且CF=1,则AB的长是( )
如图,在?ABCD中,∠BAD=120°,连接BD,作AE∥BD交CD延长线于点E,过点E作EF⊥BC交BC的延长线于点F,且CF=1,则AB的长是( )
 如图,在?ABCD中,∠BAD=120°,连接BD,作AE∥BD交CD延长线于点E,过点E作EF⊥BC交BC的延长线于点F,且CF=1,则AB的长是( )
如图,在?ABCD中,∠BAD=120°,连接BD,作AE∥BD交CD延长线于点E,过点E作EF⊥BC交BC的延长线于点F,且CF=1,则AB的长是( )| A. | 2 | B. | 1 | C. | $\sqrt{3}$ | D. | $\sqrt{2}$ |
