题目内容
5. 如图所示,直线AB、CD相交于点O,且∠AOD+∠BOC=110°,则∠AOC的度数是( )
如图所示,直线AB、CD相交于点O,且∠AOD+∠BOC=110°,则∠AOC的度数是( )| A. | 110° | B. | 115° | C. | 120° | D. | 125° |
分析 两直线相交,对顶角相等,即∠AOD=∠BOC,已知∠AOD+∠BOC=100°,可求∠AOD;又∠AOD与∠AOC互为邻补角,即∠AOD+∠AOC=180°,将∠AOD的度数代入,可求∠AOC.
解答 解:∵∠AOD与∠BOC是对顶角,
∴∠AOD=∠BOC,
又∵∠AOD+∠BOC=110°,
∴∠AOD=55°.
∵∠AOD与∠AOC互为邻补角,
∴∠AOC=180°-∠AOD=180°-55°=125°.
故选D.
点评 本题考查对顶角的性质以及邻补角的定义,是一个需要熟记的内容.

练习册系列答案
相关题目
15.某校为了备战2018体育中考,因此在八年级抽取了50名女学生进行“一分钟仰卧起坐”测试,测试的情况绘制成表格如下:
(1)通过计算算得出这50名女学生进行“一分钟仰卧起坐”的平均数是30,请写出这50名女学生进行“一分钟仰卧起坐”的众数和中位数,它们分别是28、28.
(2)学校根据测试数据规定八年级女学生“一分钟仰卧起坐”的合格标准为28次,已知该校五年级有女生250名,试估计该校五年级女生“一分钟仰卧起坐”的合格人数是多少?
| 个数 | 16 | 22 | 25 | 28 | 29 | 30 | 35 | 37 | 40 | 42 | 45 | 46 |
| 人数 | 2 | 1 | 7 | 18 | 1 | 9 | 5 | 2 | 1 | 1 | 1 | 2 |
(2)学校根据测试数据规定八年级女学生“一分钟仰卧起坐”的合格标准为28次,已知该校五年级有女生250名,试估计该校五年级女生“一分钟仰卧起坐”的合格人数是多少?
16.下列函数中,自变量x的取值范围是x>3的是( )
| A. | y=x-3 | B. | $y=\frac{1}{x-3}$ | C. | $y=\sqrt{x-3}$ | D. | y=$\frac{1}{\sqrt{x-3}}$ |
13. 为了了解学生在一年中的课外阅读量,语文老师在七年级1500名学生中采用随机抽样的方式进行了问卷调查,调查的结果分为四种情况:A:10本以下;B:10~15本;C:16~20本;D:20本以上.根据调查结果制作了下列的两幅统计图表:
为了了解学生在一年中的课外阅读量,语文老师在七年级1500名学生中采用随机抽样的方式进行了问卷调查,调查的结果分为四种情况:A:10本以下;B:10~15本;C:16~20本;D:20本以上.根据调查结果制作了下列的两幅统计图表:
根据以上信息回答下列问题:
(1)在这次调查中一共抽查了200名学生;
(2)表中x,y的值分别为:x=60,y=80;
(3)在扇形统计图中,计算C部分所对应的扇形的圆心角度数;
(4)根据抽样调查结果,请估计九年级学生一年阅读课外书20本以上的学生人数.
 为了了解学生在一年中的课外阅读量,语文老师在七年级1500名学生中采用随机抽样的方式进行了问卷调查,调查的结果分为四种情况:A:10本以下;B:10~15本;C:16~20本;D:20本以上.根据调查结果制作了下列的两幅统计图表:
为了了解学生在一年中的课外阅读量,语文老师在七年级1500名学生中采用随机抽样的方式进行了问卷调查,调查的结果分为四种情况:A:10本以下;B:10~15本;C:16~20本;D:20本以上.根据调查结果制作了下列的两幅统计图表:| 各种情况人数统计频数分布表 | ||||
| 课外阅读情况 | A | B | C | D |
| 频数 | 20 | x | y | 40 |
(1)在这次调查中一共抽查了200名学生;
(2)表中x,y的值分别为:x=60,y=80;
(3)在扇形统计图中,计算C部分所对应的扇形的圆心角度数;
(4)根据抽样调查结果,请估计九年级学生一年阅读课外书20本以上的学生人数.
20.科学家在实验中检测出某微生物约长0.000000036m,将0.000000036用科学记数法表示为( )
| A. | 3.6×10-8 | B. | 3.6×108 | C. | 3.6×10-7 | D. | 0.36×10-9 |
14.实数 x,y满足 (x-1)2+|y|=0,则点 P(x,y)在( )
| A. | 原点 | B. | x轴正半轴 | C. | 第一象限 | D. | 任意位置 |
15.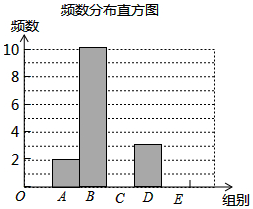 在一次社会调查活动中,小华收集到某“健步走运动”团队中一些成员一天行走的步数,并对这些数据按组距1000进行分组,并统计整理,绘制了如下尚不完整的统计图表:
在一次社会调查活动中,小华收集到某“健步走运动”团队中一些成员一天行走的步数,并对这些数据按组距1000进行分组,并统计整理,绘制了如下尚不完整的统计图表:
请根据以上信息解答下列问题:
(1)填空:a=6,c=20,m=0.3;
(2)补全频数分布直方图;
(3)若该团队共有200人,请估计其中一天行走步数不少于7500步的人数.
 在一次社会调查活动中,小华收集到某“健步走运动”团队中一些成员一天行走的步数,并对这些数据按组距1000进行分组,并统计整理,绘制了如下尚不完整的统计图表:
在一次社会调查活动中,小华收集到某“健步走运动”团队中一些成员一天行走的步数,并对这些数据按组距1000进行分组,并统计整理,绘制了如下尚不完整的统计图表:| 组别 | 步数分组 | 频数 | 频率 |
| A | 5500≤x<6500 | 2 | 0.10 |
| B | 6500≤x<7500 | 10 | 0.50 |
| C | 7500≤x<8500 | a | m |
| D | 8500≤x<9500 | 3 | 0.05 |
| E | 9500≤x<10500 | b | 0.05 |
| 合计 | 5500≤x<10500 | c | 1 |
(1)填空:a=6,c=20,m=0.3;
(2)补全频数分布直方图;
(3)若该团队共有200人,请估计其中一天行走步数不少于7500步的人数.
 端午节假时,李明一家人驾车从宝鸡到汉中游玩,如图是他们距离汉中的路程y(km)与路上耗时x(h)之间的函数关系图象.
端午节假时,李明一家人驾车从宝鸡到汉中游玩,如图是他们距离汉中的路程y(km)与路上耗时x(h)之间的函数关系图象. 我县开展“美丽新野,创卫同行”活动,某校倡议学生利用双休日参加义务劳动,为了解同学们劳动情况,学校随机调查了100名同学的劳动时间,并用得到的数据绘制了一幅不完整的统计图,根据图中信息解答下列问题:
我县开展“美丽新野,创卫同行”活动,某校倡议学生利用双休日参加义务劳动,为了解同学们劳动情况,学校随机调查了100名同学的劳动时间,并用得到的数据绘制了一幅不完整的统计图,根据图中信息解答下列问题: