题目内容
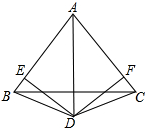 如图,已知BD=CD,∠ABD=∠ACD,DE⊥AB于点E,DF⊥AC于点F,求证:DE=DF.
如图,已知BD=CD,∠ABD=∠ACD,DE⊥AB于点E,DF⊥AC于点F,求证:DE=DF.考点:全等三角形的判定与性质,角平分线的性质
专题:证明题
分析:易证∠ABC=∠ACB,可得AB=AC,即可证明△ABD≌△ACD,可得∠BAD=∠CAD,根据角平分线性质可得DE=DF,即可解题.
解答:证明:∵BD=CD,
∴∠DBC=∠DCB,
∵∠ABD=∠ACD,
∴∠ABC=∠ACB,
∴AB=AC,
∵在△ABD和△ACD中,
,
∴△ABD≌△ACD(SAS),
∴∠BAD=∠CAD,
∴AD是∠BAC角平分线,
∴DE=DF.
∴∠DBC=∠DCB,
∵∠ABD=∠ACD,
∴∠ABC=∠ACB,
∴AB=AC,
∵在△ABD和△ACD中,
|
∴△ABD≌△ACD(SAS),
∴∠BAD=∠CAD,
∴AD是∠BAC角平分线,
∴DE=DF.
点评:本题考查了全等三角形的判定,考查了全等三角形对应角相等的性质,本题中求证△ABD≌△ACD是解题的关键.

练习册系列答案
 阳光课堂课时作业系列答案
阳光课堂课时作业系列答案
相关题目
已知(a3b-4)2÷(-ab-3)3=3,则a9b3的值是( )
| A、-9 | B、9 | C、27 | D、-27 |
已知D是△ABC内一点,且BD=CD,下列说法正确的是( )
| A、点D是三角形三边垂直平分线的交点 |
| B、点D是三角形三条角平分线的交点 |
| C、点D在BC的垂直平分线上 |
| D、点D在∠A的平分线上 |
 如图,已知AD是△ABC的中线,且AE:EB=1:6,射线CF交AD于点F,则AF:FD=
如图,已知AD是△ABC的中线,且AE:EB=1:6,射线CF交AD于点F,则AF:FD=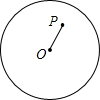 如图,P是半径为4cm的圆内一点,OP=2cm,过点P的弦与圆弧组成弓形,当过点P的弦垂直于OP时,弦与其所对的劣弧组成的弓形面积最小,那么最小弓形面积是多少?
如图,P是半径为4cm的圆内一点,OP=2cm,过点P的弦与圆弧组成弓形,当过点P的弦垂直于OP时,弦与其所对的劣弧组成的弓形面积最小,那么最小弓形面积是多少?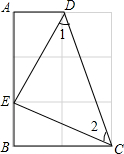 如图,四边形ABCD中,如果∠A=∠B=90°,∠1=∠2=45°,使A,E,B在同一直线上,连接CD,并且AD=BE.
如图,四边形ABCD中,如果∠A=∠B=90°,∠1=∠2=45°,使A,E,B在同一直线上,连接CD,并且AD=BE.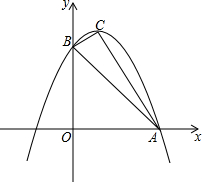 如图,已知抛物线y=ax2+bx+c与x轴的一个交点为A(3,0),与y轴的交点为B(0,3),其顶点为C,对称轴为x=1.
如图,已知抛物线y=ax2+bx+c与x轴的一个交点为A(3,0),与y轴的交点为B(0,3),其顶点为C,对称轴为x=1.