题目内容
7.已知二次函数y=-$\frac{3}{2}{x^2}$+2x+1,当y随x的增大而增大时,x的取值范围是x<$\frac{2}{3}$.分析 函数图象开口向下,求出二次函数的对称轴,即可知道x取何值时,y随x的增大而增大.
解答 解:∵二次函数y=-$\frac{3}{2}{x^2}$+2x+1,图象开口向下,对称轴x=-$\frac{2}{2×(-\frac{3}{2})}$=$\frac{2}{3}$,
∴当x<$\frac{2}{3}$时,y随x的增大而增大.
故答案为:x<$\frac{2}{3}$.
点评 本题考查了二次函数的性质,能根据解析式推知函数图象是解题的关键,另外要能准确计算出函数的对称轴.

练习册系列答案
 名校练考卷期末冲刺卷系列答案
名校练考卷期末冲刺卷系列答案
相关题目
15.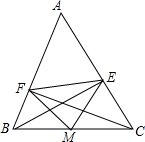 如图,在△ABC中,CF⊥AB于点F,BE⊥AC于点E,M为BC的中点,EF=5,BC=8,则△EFM的周长及图中的等腰三角形个数分别是( )
如图,在△ABC中,CF⊥AB于点F,BE⊥AC于点E,M为BC的中点,EF=5,BC=8,则△EFM的周长及图中的等腰三角形个数分别是( )
 如图,在△ABC中,CF⊥AB于点F,BE⊥AC于点E,M为BC的中点,EF=5,BC=8,则△EFM的周长及图中的等腰三角形个数分别是( )
如图,在△ABC中,CF⊥AB于点F,BE⊥AC于点E,M为BC的中点,EF=5,BC=8,则△EFM的周长及图中的等腰三角形个数分别是( )| A. | 21、2 | B. | 18、3 | C. | 13、4 | D. | 13、5 |
2.二次函数y=x2-6x+c的图象经过A(-1,y1),B(3,y2),C(4,y3)三点,则y1,y2,y3的大小关系是( )
| A. | y2>y1>y3 | B. | y1>y2>y3 | C. | y1>y3>y2 | D. | y3>y1>y2 |
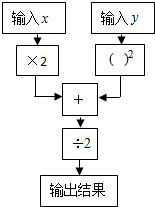 如图是一个数值转换机的示意图,若输入x的值为4,y的值为-2,则输出的结果为2.
如图是一个数值转换机的示意图,若输入x的值为4,y的值为-2,则输出的结果为2.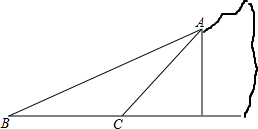 因山体滑坡,需将一段50米长的滑坡体清除,滑坡体横截面是如图所示的△ABC.测得堡坎坡面AC的坡度是1:1,滑坡体坡面AB的坡角是30°,滑坡体底宽BC=13米.
因山体滑坡,需将一段50米长的滑坡体清除,滑坡体横截面是如图所示的△ABC.测得堡坎坡面AC的坡度是1:1,滑坡体坡面AB的坡角是30°,滑坡体底宽BC=13米. 在数轴上表示下列各数:2,-1,0,-$\frac{5}{4}$,-3.5,3,并用“<”将它们连接起来.
在数轴上表示下列各数:2,-1,0,-$\frac{5}{4}$,-3.5,3,并用“<”将它们连接起来.