题目内容
15.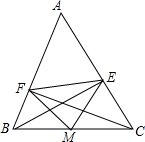 如图,在△ABC中,CF⊥AB于点F,BE⊥AC于点E,M为BC的中点,EF=5,BC=8,则△EFM的周长及图中的等腰三角形个数分别是( )
如图,在△ABC中,CF⊥AB于点F,BE⊥AC于点E,M为BC的中点,EF=5,BC=8,则△EFM的周长及图中的等腰三角形个数分别是( )| A. | 21、2 | B. | 18、3 | C. | 13、4 | D. | 13、5 |
分析 根据直角三角形斜边上的中线等于斜边的一半得到FM=$\frac{1}{2}$BC=4,ME=$\frac{1}{2}$BC=4,求出△EFM的周长,根据等腰三角形的判定求出等腰三角形个数.
解答 解:∵CF⊥AB于点F,BE⊥AC于点E,M为BC的中点,
∴FM=$\frac{1}{2}$BC=4,ME=$\frac{1}{2}$BC=4,
∴△EFM的周长=FM+EM+EF=13,
△FMB、△EMC、△FME、△BME、△FMC是等腰三角形,
故选:D.
点评 本题考查的是直角三角形的性质和等腰三角形的判断,掌握直角三角形斜边上的中线等于斜边的一半是解题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
5.平方得16的数是( )
| A. | 4 | B. | -4 | C. | ±4 | D. | ±16 |
6.已知在数轴上A点表示-2,若将A点向右边平移3个单位后,再向左平移2个单位,则此时A点表示的有理数是( )
| A. | 1 | B. | 0 | C. | -2 | D. | -1 |
10.二次根式$\sqrt{{a}^{2}}$=-a的条件是( )
| A. | a>0 | B. | a<0 | C. | a≤0 | D. | a是任意实数 |
5.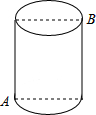 如图,一圆柱高8cm,底面半径为$\frac{6}{π}$ cm,一只蚂蚁从点A爬到点B处吃食,要爬行的最短路程是( )
如图,一圆柱高8cm,底面半径为$\frac{6}{π}$ cm,一只蚂蚁从点A爬到点B处吃食,要爬行的最短路程是( )
 如图,一圆柱高8cm,底面半径为$\frac{6}{π}$ cm,一只蚂蚁从点A爬到点B处吃食,要爬行的最短路程是( )
如图,一圆柱高8cm,底面半径为$\frac{6}{π}$ cm,一只蚂蚁从点A爬到点B处吃食,要爬行的最短路程是( )| A. | 6cm | B. | 8cm | C. | 10cm | D. | 12cm |