题目内容
2.二次函数y=x2-6x+c的图象经过A(-1,y1),B(3,y2),C(4,y3)三点,则y1,y2,y3的大小关系是( )| A. | y2>y1>y3 | B. | y1>y2>y3 | C. | y1>y3>y2 | D. | y3>y1>y2 |
分析 根据函数解析式的特点,其对称轴为x=3,图象开口向上,有最小值;根据二次函数图象的对称性可判断y3>y1;于是y1>y3>y2.
解答 解:∵二次函数y=x2-6x+c中a=1>0,
∴抛物线开口向上,有最小值.
∵x=-$\frac{b}{2a}$=3,
∴B(3,y2)是顶点,y2最小,
∵由二次函数图象的对称性可知y1>y3,
∴y1>y3>y2.
故选C.
点评 本题考查的是二次函数图象上点的坐标特点,熟知二次函数图象上各点的坐标一定适合此函数的解析式是解答此题的关键.

练习册系列答案
相关题目
10.二次根式$\sqrt{{a}^{2}}$=-a的条件是( )
| A. | a>0 | B. | a<0 | C. | a≤0 | D. | a是任意实数 |
17.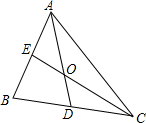 如图,在△ABC中,点O是其重心,连接AO,CO并延长,分别交BC,AB于D,E两点,则下列说法中一定正确的是( )
如图,在△ABC中,点O是其重心,连接AO,CO并延长,分别交BC,AB于D,E两点,则下列说法中一定正确的是( )
 如图,在△ABC中,点O是其重心,连接AO,CO并延长,分别交BC,AB于D,E两点,则下列说法中一定正确的是( )
如图,在△ABC中,点O是其重心,连接AO,CO并延长,分别交BC,AB于D,E两点,则下列说法中一定正确的是( )| A. | ∠BAD=∠CAD | B. | AE=CD | C. | OA=OC | D. | BD=CD |
14.将面积为a2的正方形边长增加2,则正方形的面积增加了( )
| A. | 4 | B. | 2a+4 | C. | 4a+4 | D. | 4a |
 如图,是由几个相同的小正方体组成的几何体,则它的左视图是( )
如图,是由几个相同的小正方体组成的几何体,则它的左视图是( )


